
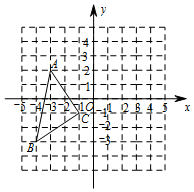
 如圖,(1)畫出△ABC先向右平移4個單位,再向上平移1個單位后的圖形△A'B'C';
如圖,(1)畫出△ABC先向右平移4個單位,再向上平移1個單位后的圖形△A'B'C';分析 (1)根據三角形平移的性質畫出平移后的△A′B′C′即可;
(2)利用待定系數法求出直線A′C′的解析式即可;
(3)先根據勾股定理的逆定理判斷出△ABC的形狀,進而可得出結論.
解答 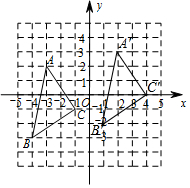 解:(1)如圖,△A′B′C′即為所求;
解:(1)如圖,△A′B′C′即為所求;
(2)設直線A′C′的解析式為y=kx+b(k≠0),
∵A′(2,3),C′(4,0),
∴$\left\{\begin{array}{l}{2k+b=3}\\{4k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{3}{2}}\\{b=\frac{9}{2}}\end{array}\right.$,
∴直線A′C′的解析式為:y=-$\frac{3}{2}$x+$\frac{9}{2}$;
(3)∵AB2=12+52=26,AC2=22+32=13,BC2=22+32=13,
∴△ABC是等腰直角三角形,
∴△ABC中AB邊上的高=$\frac{\sqrt{13}×\sqrt{13}}{\sqrt{26}}$=$\frac{\sqrt{26}}{2}$.
點評 本題考查的是作圖-平移變換及勾股定理的逆定理,熟知圖形平移不變性的性質是解答此題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
 為了解國家提倡的“陽光體育運動”的實施情況,將某校中的40名學生一周的體育鍛煉時間繪制成了如圖所示的條形統計圖,根據統計圖提供的數據,該校40名同學一周參加體育鍛煉時間的眾數與中位數分別是( )
為了解國家提倡的“陽光體育運動”的實施情況,將某校中的40名學生一周的體育鍛煉時間繪制成了如圖所示的條形統計圖,根據統計圖提供的數據,該校40名同學一周參加體育鍛煉時間的眾數與中位數分別是( )| A. | 8,8 | B. | 8,9 | C. | 9,8 | D. | 10,9 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,∠MON=30°,且OP平分∠MON,過點P作PQ∥OM交ON于點Q.若點P到OM的距離為2,則OQ的長為( )
如圖,∠MON=30°,且OP平分∠MON,過點P作PQ∥OM交ON于點Q.若點P到OM的距離為2,則OQ的長為( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 3 | 2 | 1 | 0 | -1 | -2 |
| A. | x>0 | B. | x<0 | C. | x>1 | D. | x<1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
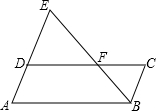 如圖,點F是?ABCD的邊CD上一點,直線BF交AD的延長線于點E,則下列結論錯誤的是( )
如圖,點F是?ABCD的邊CD上一點,直線BF交AD的延長線于點E,則下列結論錯誤的是( )| A. | $\frac{ED}{EA}$=$\frac{DF}{AB}$ | B. | $\frac{DE}{CB}$=$\frac{EF}{FB}$ | C. | $\frac{BF}{BE}$=$\frac{BC}{AE}$ | D. | $\frac{BC}{DE}$=$\frac{BF}{BE}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 42×103 | B. | 4.2×105 | C. | 0.42×105 | D. | 4.2×104 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com