
【題目】已知ABC在平面直角坐標系內,滿足:點A在y軸正半軸上移動,點B在x軸負半軸上移動,點C為y軸右側一動點.

點A0,a和點Bb,0坐標恰好滿足:![]() ,直接寫出a,b的值.
,直接寫出a,b的值.
⑵如圖①,當點C在第四象限時,若AM、AO將BAC三等分,BM、BO將ABC三等分,在A、B、C的運動過程中,試求出C和M的關系.
⑶探究:
(i)如圖②,當點C在第四象限時,若AM平分CAO,BM平分CBO,在A、B、C的運動過程中,C和M是否存在確定的數量關系?若存在,請證明你的結論;若不存在,請說明理由.
(ii)如圖③,當點C在第一象限時,且在(i)中的條件不變的前提下,C和M又有何數量關系?證明你的結論.
【答案】(1)a=-2,b=3; (2) ∠M-∠C=90°(或∠M+∠C=180°,即∠M與∠C互補.);(3)(i)2∠M-∠C=90°; (ii)2∠M-∠C=90°.
【解析】
(1)根據非負數的性質得到關于a,b的二元一次方程組,解方程組即可;
(2)根據三等分線的性質可得出∠CAB=3∠MAB,∠CBA=3∠MBA,∠OAB=2∠MAB,∠OBA=2∠MBA.根據三角形的內角和等于180°,可求出∠OAB+∠OBA=90°,從而得出∠MAB+∠MBA=45°,∠CAB+∠CBA=135°,再次根據三角形的內角和等于180°分別求出∠M=135°,∠C=45°,從而得出∠M-∠C=90°.
(3)根據角平分線的定義和三角形的內角和定理可得出結論2∠M-∠C=90°.
解:(1)∵![]()
∴![]() ,解得:
,解得:![]()
即a,b的值分別為2,-3.
(2)如圖1.∠M-∠C=90°.理由如下:
∵AM、AO將BAC三等分,
∴∠CAB=3∠MAB,∠MAB=![]() ∠OAB.
∠OAB.
∵BM、BO將ABC三等分,
∴∠CBA=3∠MBA,∠MBA=![]() ∠OBA.
∠OBA.
∵∠OAB+∠OBA=90°,
∴∠MAB+∠MBA=![]() 90°=45°,
90°=45°,
∵∠MAB+∠MBA+∠M=180°,
∴∠M=135°.
∵∠MAB+∠MBA=45°,
∴∠CBA+∠CAB=3(∠MAB+∠MBA)=3![]() 45°=135°,
45°=135°,
∵∠CBA+∠CAB+∠C=180°.
∴∠C=45°.
∴∠M-∠C=90°.(或∠M+∠C=180°,即∠M與∠C互補.)
(3)(i)如圖2.∵AM平分CAO,
∴∠CAO=2∠MAO.
∵BM平分CBO,
∴CBO=2MBO.
∴∠CAO+CBO=2∠MAO+2MBO=2(∠MAO+MBO)
∵∠C+∠CAO+∠OAB+∠OBA+∠CBO=180°,∠OAB+∠OBA=90°,
∴∠C+∠CAO+∠CBO=180°-90°=90°.
∴∠C+2(∠MAO+MBO)= 90°.
∵∠M+∠MAO+∠OAB+∠OBA+∠MBO=180°,
∴∠M+∠MAO+∠MBO=180°-(∠OAB+∠OBA)=180°-90°=90°.
∴∠MAO+∠MBO=90°-∠M
∵∠C+2(∠MAO+MBO)= 90°,
∴∠C+2(90°-∠M) = 90°.
即2∠M-∠C=90°.
(ii)如圖3. ∵AM平分CAO,
∴∠CAO=2∠MAO.
∵BM平分CBO,
∴CBO=2MBO.
∴∠CAO-CBO=2(∠MAO-MBO)
∵∠C+∠CAO+∠0AB+∠OBA-∠CBO=180°,且∠OAB+∠OBA=90°,
∴∠C+∠CAO-∠CBO=90°.
∴∠C+2(∠MAO-MBO)= =90°.
∵∠M+∠MAO+∠0AB+∠OBA-∠MBO=180°,
∴∠M+∠MAO-∠MBO=90°,
∴∠MAO-∠MBO=90°-∠M.
∴∠C+2(90°-∠M)= 90°,
即2∠M-∠C=90°.


科目:初中數學 來源: 題型:
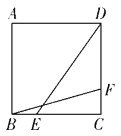
【題目】如圖,在邊長為4的正方形ABCD中,點E、F分別是邊BC、CD上的動點,且BE=CF,連接BF、DE,則BF+DE的最小值為()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,下列由5個結論:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1).其中正確的結論有_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】等腰Rt△ACB,∠ACB=90°,AC=BC,點A、C分別在x軸、y軸的正半軸上.

(1)如圖1,求證:∠BCO=∠CAO
(2)如圖2,若OA=5,OC=2,求B點的坐標
(3)如圖3,點C(0,3),Q、A兩點均在x軸上,且S△CQA=18.分別以AC、CQ為腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM,連接MN交y軸于P點,OP的長度是否發(fā)生改變?若不變,求出OP的值;若變化,求OP的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四張質地、大小、背面完全相同的卡片上,正面分別畫有平行四邊形、矩形、等腰三角形、菱形四個圖案.現把它們的正面向下隨機擺放在桌面上,從中任意抽出一張,則抽出的卡片正面圖案是中心對稱圖形的概率為___________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=ax2+bx+c交x軸于A、B兩點,交y軸于點C,已知拋物線的對稱軸為x=1,B(3,0),C(0,-3),
(1)求二次函數y=ax2+bx+c的解析式;
(2)在拋物線對稱軸上是否存在一點P,使點P到B、C兩點距離之差最大?若存在,求出P點坐標;若不存在,請說明理由;
(3)平行于x軸的一條直線交拋物線于M,N兩點,若以MN為直徑的圓恰好與x軸相切,求此圓的半徑.

查看答案和解析>>
科目:初中數學 來源: 題型:
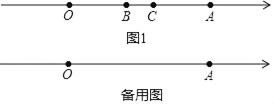
【題目】已知數軸上,點O為原點,點A對應的數為11,點B對應的數為b,點C在點B右側,長度為3個單位的線段BC在數軸上移動,
(1)如圖1,當線段BC在O,A兩點之間移動到某一位置時,恰好滿足線段AC=OB,求此時b的值;
(2)線段BC在數軸上沿射線AO方向移動的過程中,是否存在AC﹣OB=![]() AB?若存在,求此時滿足條件的b的值;若不存在,說明理由.
AB?若存在,求此時滿足條件的b的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com