【題目】新型冠狀病毒肺炎疫情發生后，全社會積極參與疫情防控工作，某市為了盡快完成100萬只口罩的生產任務，安排甲、乙兩個大型工廠完成．已知甲廠每天能生產口罩的數量是乙廠每天能生產口罩的數量的1.5倍，并且在獨立完成60萬只口罩的生產任務時，甲廠比乙廠少用5天，求甲、乙兩廠每天能生產口罩多少萬只？
科目：初中數學 來源： 題型：
【題目】（本題10分）如圖，在平面直角坐標系xOy中，直線
與y軸交于點C，與x軸交于點B，拋物線
經過B、C兩點，與x軸的正半軸交于另一點A，且OA ：OC="2" ：7．
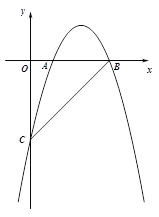
（1）求拋物線的解析式；
（2）點D為線段CB上，點P在對稱軸的右側拋物線上，PD=PB，當tan∠PDB＝２，求P點的坐標；
（3）在（2）的條件下，點Q（7，m）在第四象限內，點R在對稱軸的右側拋物線上，若以點P、D、Q、R為頂點的四邊形為平行四邊形，求點Q、R的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
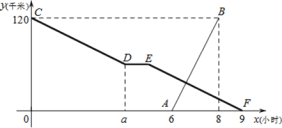
【題目】甲、乙兩地相距 120 千米，小張騎自行車從甲地出發勻速駛往乙地，出發 a小時開始休息，1 小時后仍按原速繼續行駛．小李比小張晚出發一段時間，騎摩托車從乙地勻速駛往甲地，圖中折線 CD－DE－EF，線段 AB 分別表示小張、小李與乙地的距離 y（千米）與小張出發時間 x（小時）之間的函數關系圖象．
（1）小李到達甲地后，再經過 小時小張到達乙地；小張騎自行車的速度是 千米/時；
（2）當 a＝4 時，求小張與乙地的距離 y乙 與小張出發的時間 x（小時）之間的函數關系式；
（3）若小張恰好在休息期間與小李相遇，請直接寫出 a 的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
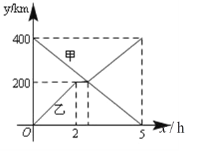
【題目】甲，乙兩輛汽車分別從A，B兩地同時出發，沿同一條公路相向而行，乙車出發2h后休息，與甲車相遇后，繼續行駛．設甲，乙兩車與B地的路程分別為y甲(km)，y乙 (km)，行駛的時間為x(h)，y甲，y乙與x之間的函數圖象如圖所示，結合圖象解答下列問題：
（1）乙車休息了多長時間；
（2）求乙車與甲車相遇后y乙與x的函數解析式，并寫出自變量x的取值范圍；
（3）當兩車相距40km時，求出x的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，
與
軸交于點C，與
軸的正半軸交于點K，過點
作
軸交拋物線于另一點B，點
在軸的負半軸上，連結
交軸于點A，若
．
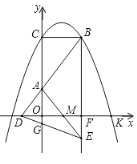
（1）用含
的代數式表示
的長；
（2）當
時，判斷點是否落在拋物線上，并說明理由；
（3）過點
作
軸交軸于點
延長
至
，使得
連結
交軸于點
連結AE交軸于點
若
的面積與
的面積之比為
則求出拋物線的解析式．
查看答案和解析>>
科目：初中數學 來源： 題型：
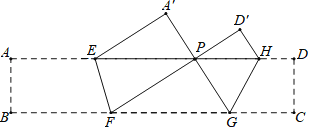
【題目】如圖，把某矩形紙片ABCD沿EF，GH折疊（點E，H在AD邊上，點F，G在BC邊上），使點B和點C落在AD邊上同一點P處，A點的對稱點為A′點，D點的對稱點為D′點，若∠FPG＝90°，△A′EP的面積為8，△D′PH的面積為2，則矩形ABCD的面積等于 （ ）
A.
B.
C.
D.16＋12
查看答案和解析>>
科目：初中數學 來源： 題型：
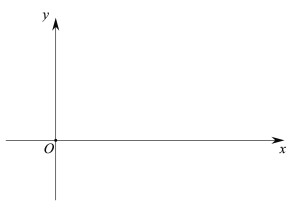
【題目】如圖，平面直角坐標系，拋物線
（
，
）與
軸交于A、B兩點（A在B左側），與
軸交于點C，過拋物線的頂點P且與軸平行的直線
交BC于點D，且滿足BD：CD=3：2，
（1）若∠ACB=90°，求拋物線解析式；
（2）問OC和DP能否相等？若能，求出拋物線解析式，若不能，說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
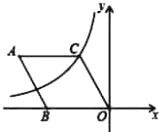
【題目】如圖，在菱形ABOC中，AB＝2，∠A＝60°，菱形的一個頂點C在反比例函數y＝
（k≠0）的圖象上，則反比例函數的解析式為（ ）
A.y＝
B.y＝
C.y＝
D.y＝
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】2020年3月至5月，某校開展了一系列居家閱讀活動．學生利用“宅家”時光，在書海中遨游，從閱讀中獲得精神慰藉和自我提升．為了解學生居家閱讀的情況，學校從七、八兩個年級各隨機抽取50名學生，進行了居家閱讀情況調查．下面給出了部分數據信息：
．兩個年級學生平均每周閱讀時長
（單位：小時）的頻數分布直方圖如下（數據分成4組：
，
，
，
）：
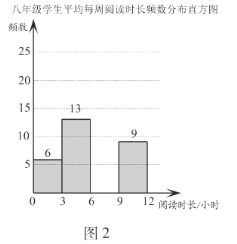
b．七年級學生平均每周閱讀時長在這一組的是：6 6 7 7 7 7 7 8 8 8 8 8 8 8 8 8
c．兩個年級學生平均每周閱讀時長的平均數、中位數、眾數、方差如下：
平均數 | 中位數 | 眾數 | 方差 | |
七年級 | 6.3 |
| 8 | 7.0 |
八年級 | 6.0 | 7 | 7 | 6.3 |
根據以上信息，回答下列問題：
（1）補全圖2；
（2）寫出表中
的值；
（3）返校后，學校計劃將平均每周閱讀時長不低于9小時的學生授予“閱讀之星”稱號．小麗說：“根據頻數分布直方圖中的數據信息，估計七年級約有20%的學生獲得該稱號，八年級約有18%的學生獲得該稱號，所以七年級獲得該稱號的人數一定比八年級獲得該稱號的人數多．”你認為她的說法________（填入“正確”或“錯誤”）；
（4）請你結合數據對兩個年級的居家閱讀情況進行評價．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
