
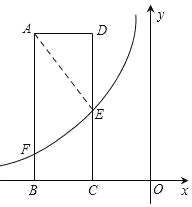
【題目】如圖,矩形![]() 的兩邊
的兩邊![]() ,
,![]() 的長分別為3,8,且點
的長分別為3,8,且點![]() ,
,![]() 均在
均在![]() 軸的負半軸上,
軸的負半軸上,![]() 是
是![]() 的中點,反比例函數
的中點,反比例函數![]() 的圖象經過點
的圖象經過點![]() ,與
,與![]() 交于點
交于點![]() .
.

(1)若點![]() 坐標為
坐標為![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,且點
,且點![]() 的橫坐標為
的橫坐標為![]() ,則點
,則點![]() 的橫坐標為______(用含
的橫坐標為______(用含![]() 的代數式表示),點
的代數式表示),點![]() 的縱坐標為______,反比例函數的表達式為______.
的縱坐標為______,反比例函數的表達式為______.
【答案】(1)![]() ;(2)
;(2)![]() ,1,
,1,![]() .
.
【解析】
(1)根據矩形的性質,可得A,E的坐標,根據待定系數法即可求解;
(2)根據勾股定理,可得AE的長,根據線段的和差,可得FB,可得F的占比,根據待定系數法,可得m的值,即可求解.
解:(1)∵四邊形![]() 是矩形,
是矩形,
∴![]() ,即
,即![]() 軸,
軸,
![]() ,
,![]() ,
,
∵![]() 是
是![]() 的中點,
的中點,
∴![]() ,
,
∵點![]() 坐標為
坐標為![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴點![]() 的坐標為
的坐標為![]() .
.
把點![]() 代入反比例函數
代入反比例函數![]() 得,
得,![]() ,∴
,∴![]() .
.
(2)如圖,連接AE,∵點E的橫坐標為a,BC=3
∴點F的橫坐標為a-3,
又∵在Rt△ADE中,AE=![]()
∴AF=AE+2=7,BF=8-7=1
∴點F的縱坐標為1,
∴E(a,4),F(a-3,1)
∵反比例函數經過E,F
∴4a=1(a-3)
解得a=-1,
∴E(-1,4)
∴k=-4,
故反比例函數的解析式為![]()


科目:初中數學 來源: 題型:
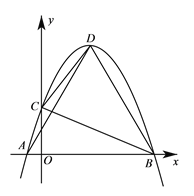
【題目】如圖,拋物線y=-![]()
![]() +mx+m+
+mx+m+![]() 與x軸相交于點A、B(點A在B的左側)與y軸相交于點C,頂點D在第一象限.
與x軸相交于點A、B(點A在B的左側)與y軸相交于點C,頂點D在第一象限.
(1)求頂點D的坐標(用m 的代數式表示);
(2)當60°≤∠ADB≤90°時,求m的變化范圍;
(3)當△BCD的面積與△ABC的面積相等時,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
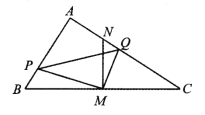
【題目】在△ABC 中,∠BAC=90°,AB<AC,M 是 BC 邊的中點,MN⊥BC交 AC 于點 N,動點 P 在線段 BA 上以每秒![]() cm 的速度由點 B 向點 A 運動.同時, 動點 Q 在線段 AC 上由點 N 向點 C 運動,且始終保持 MQ⊥MP. 一個點到終點時,兩個點同時停止運動.設運動時間為 t 秒(t>0).
cm 的速度由點 B 向點 A 運動.同時, 動點 Q 在線段 AC 上由點 N 向點 C 運動,且始終保持 MQ⊥MP. 一個點到終點時,兩個點同時停止運動.設運動時間為 t 秒(t>0).
(1)△PBM 與△QNM 相似嗎?請說明理由;
(2)若∠ABC=60°,AB=4 ![]() cm.
cm.
①求動點 Q 的運動速度;
②設△APQ 的面積為 s(cm2),求 S 與 t 的函數關系式.(不必寫出 t 的取值范圍)
(3)探求 BP、PQ、CQ 三者之間的數量關系,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
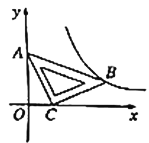
【題目】在平面直角坐標系![]() 中,將一塊含有
中,將一塊含有![]() 角的直角三角板如圖放置,直角頂點
角的直角三角板如圖放置,直角頂點![]() 的坐標為
的坐標為![]() ,頂點
,頂點![]() 的坐標為
的坐標為![]() ,頂點
,頂點![]() 恰好落在第一象限的雙曲線上,現將直角三角板沿
恰好落在第一象限的雙曲線上,現將直角三角板沿![]() 軸正方向平移,當頂點
軸正方向平移,當頂點![]() 恰好落在該雙曲線上時停止運動,則此時點
恰好落在該雙曲線上時停止運動,則此時點![]() 的對應點
的對應點![]() 的坐標為( )
的坐標為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場購進甲、乙兩種空調共40臺.已知購進一臺甲種空調比購進一臺乙種空調進價多0.2萬元;用36萬元購進乙種空調數量是用18萬元購進甲種空調數量的4倍.請解答下列問題:
(1)求甲、乙兩種空調每臺進價各是多少萬元?
(2)若商場預計投入資金不多于11.5萬元用于購買甲、乙兩種空調,且購進甲種空調至少14臺,商場有哪幾種購進方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線y=mx2﹣4mx+4m+4(m≠0)的頂點為P.P,M兩點關于原點O成中心對稱.
(1)求點P,M的坐標;
(2)若該拋物線經過原點,求拋物線的表達式;
(3)在(2)的條件下,將拋物線沿x軸翻折,翻折后的圖象在0≤x≤5的部分記為圖象H,點N為拋物線對稱軸上的一個動點,經過M,N的直線與圖象H有兩個公共點,結合圖象求出點N的縱坐標n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中央電視臺的“中國詩詞大賽”節目文化品位高,內容豐富,某校初二年級模擬開展“中國詩詞大賽”比賽,對全年級同學成績進行統計后分為“優秀”、“良好”、“一般”、“較差”四個等級,并根據成績繪制成如下兩幅不完整的統計圖,請結合統計圖中的信息,回答下列問題:

(1)扇形統計圖中“優秀”所對應的扇形的圓心角為 度,并將條形統計圖補充完整.
(2)此次比賽有四名同學活動滿分,分別是甲、乙、丙、丁,現從這四名同學中挑選兩名同學參加學校舉行的“中國詩詞大賽”比賽,請用列表法或畫樹狀圖法,求出選中的兩名同學恰好是甲、丁的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】己知:如圖1,⊙O的半徑為2, BC是⊙O的弦,點A是⊙O上的一動點。
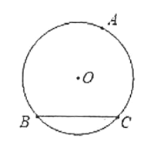
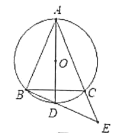
圖1 圖2
(1)當△ABC的面積最大時,請用尺規作圖確定點A位置(尺規作圖只保留作圖痕跡, 不需要寫作法);
(2)如圖2,在滿足(1)條件下,連接AO并延長交⊙O于點D,連接BD并延長交AC 的延長線于點E,若∠BAC=45° ,求AC2+CE2的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com