
【題目】四邊形![]() 是
是![]() 的內接四邊形,
的內接四邊形,![]() ,
,![]() ,垂足為
,垂足為![]() .
.
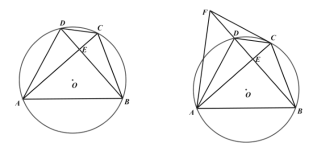
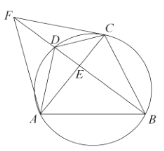
(1)如圖1,求證:![]() ;
;
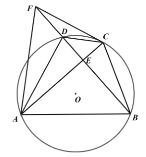
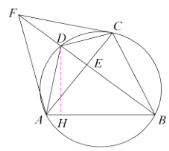
(2)如圖2,點![]() 在
在![]() 的延長線上,且
的延長線上,且![]() ,連接
,連接![]() 、
、![]() ,求證:
,求證:![]() ;
;
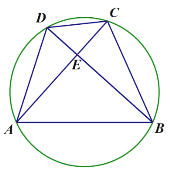
(3)如圖3,在(2)的條件下,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)證明見解析;(2)證明見解析;(3)![]() .
.
【解析】
(1)由圓周角定理得出∠DAC=∠CBD,證出∠ACB=90°∠CBD,由等腰三角形的性質得出∠ABC=∠ACB=90°∠CBD,得出∠BAC=180°2∠ABC=2∠CBD,即可得出結論;
(2)由等腰三角形的性質得出∠FCD=∠CFD,證出∠CFD=∠CAD,進而得出∠CFD=∠CBD,即可得出結論;
(3)證出AB=AF=AC=10設AE=x,CE=10x,由勾股定理得出AB2AE2=BC2CE2,得出102x2=(4![]() )2(10x)2,求出AE=6,CE=4,由勾股定理得出BE=8,由三角函數定義得出
)2(10x)2,求出AE=6,CE=4,由勾股定理得出BE=8,由三角函數定義得出![]() ,求出DE=3,由勾股定理得出AD=3
,求出DE=3,由勾股定理得出AD=3![]() ,過點D作DH⊥AB,垂足為H,由面積法求出DH=
,過點D作DH⊥AB,垂足為H,由面積法求出DH=![]() ,由三角函數定義即可得出答案.
,由三角函數定義即可得出答案.
(1)證明:如圖1,
∵弧![]() 弧
弧![]()
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,∴
,∴![]() ,
,
∴![]()
∴![]()
(2)證明:如圖2,∵![]()
∴![]()
∴![]()
∴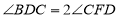
∵![]() ,
,![]()
∴![]()
∵![]()
∴![]()
∴![]()
(3)解:如圖3,∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() 垂直平分
垂直平分![]() ,
,
∴![]()
設![]() ,
,![]() ,
,
在![]() 中,
中,![]()
在![]() 中,
中,![]() ,
,
∴![]() ,∵
,∵![]()
∴![]() ,解得
,解得![]()
∴![]() ,
,![]()
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
∴![]()
在![]() 中,
中,![]()
∴![]()
過點![]() 作
作![]() ,垂足為
,垂足為![]()
∴![]()
![]()
∴![]()
在![]() 中,
中,
∴![]() .
.


科目:初中數學 來源: 題型:
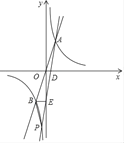
【題目】如圖,過原點O的直線與雙曲線y=![]() 交于上A(m,n)、B,過點A的直線交x軸正半軸于點D,交y軸負半軸于點E,交雙曲線y=
交于上A(m,n)、B,過點A的直線交x軸正半軸于點D,交y軸負半軸于點E,交雙曲線y=![]() 于點P.
于點P.
(1)當m=2時,求n的值;
(2)當OD:OE=1:2,且m=3時,求點P的坐標;
(3)若AD=DE,連接BE,BP,求△PBE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1個單位長度的小正方形組成的網格中,給出了格點△ABC(頂點是網格線的交點)和點A1.
(1)畫出一個格點△A1B1C1,并使之是由△ABC平移后得到,且A與A1是對應點;
(2)畫出點B關于直線AC的對稱點D,并指出AD可以看作由AB繞A點經過怎樣的旋轉而得的;
(3)將△ABC繞點A逆時針旋轉一定角度,使得AB落在(2)中的線段AD的位置,請作出旋轉后的三角形,并求在這一旋轉過程中△ABC掃過的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一次函數 y=kx-2 的圖象與 x 軸、y 軸分別交于 A,B 兩點,與反比例函數![]() 的圖象交于點 C,且 AB=AC,則 k 的值為( )
的圖象交于點 C,且 AB=AC,則 k 的值為( )
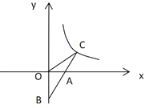
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在 Rt△ABC 中,∠C=90°,AD 平分∠BAC 交 BC 于點 D,O 為 AB 上一點,經過點 A、D 的⊙O 分別交 AB、AC 于點 E、F,
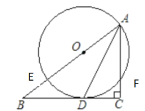
(1)求證:BC 是⊙O 切線;
(2)設 AB=m,AF=n,試用含 m、n 的代數式表示線段 AD 的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
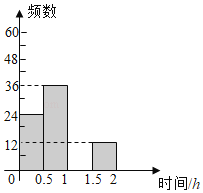
【題目】揚州市“五個一百工程“在各校普遍開展,為了了解某校學生每天課外閱讀所用的時間情況,從該校學生中隨機抽取了部分學生進行問卷調查,并將結果繪制成如圖不完整的頻數分布表和頻數分布直方圖.
每天課外閱讀時間t/h | 頻數 | 頻率 |
0<t≤0.5 | 24 | |
0.5<t≤1 | 36 | 0.3 |
1<t≤1.5 | 0.4 | |
1.5<t≤2 | 12 | b |
合計 | a | 1 |
根據以上信息,回答下列問題:
(1)表中a= ,b= ;
(2)請補全頻數分布直方圖;
(3)若該校有學生1200人,試估計該校學生每天課外閱讀時間超過1小時的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
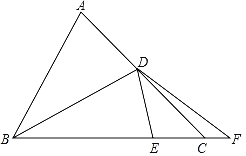
【題目】△ABC中,∠ACB=45°,D為AC上一點,AD=5![]() ,連接BD,將△ABD沿BD翻折至△EBD,點A的對應點E點恰好落在邊BC上.延長BC至點F,連接DF,若CF=2,tan∠ABD=
,連接BD,將△ABD沿BD翻折至△EBD,點A的對應點E點恰好落在邊BC上.延長BC至點F,連接DF,若CF=2,tan∠ABD=![]() ,則DF長為( )
,則DF長為( )
A.![]() B.
B.![]() C.5
C.5![]() D.7
D.7![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
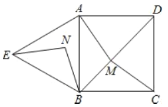
【題目】如圖,四邊形![]() 是正方形,
是正方形,![]() 是等邊三角形,
是等邊三角形,![]() 為對角線
為對角線![]() (不含
(不含![]() 點)上任意一點,將
點)上任意一點,將![]() 繞點
繞點![]() 逆時針旋轉60°得到
逆時針旋轉60°得到![]() ,連接
,連接![]() 、
、![]() 、
、![]() .
.
(1)求證![]() ;
;
(2)①當![]() 點在何處時,
點在何處時,![]() 的值最小;
的值最小;
②當![]() 點在何處時,
點在何處時,![]() 的值最小,并說明理由;
的值最小,并說明理由;
(3)當![]() 的最小值為
的最小值為![]() 時,求正方形的邊長.
時,求正方形的邊長.
查看答案和解析>>
科目:初中數學 來源: 題型:
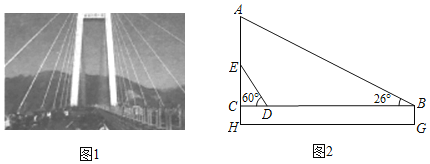
【題目】北盤江大橋坐落于云南宜威與貴州水城交界處,橫跨云貴兩省,為目前世界第一高橋圖1是大橋的實物圖,圖2是從圖1中引申出的平面圖,測得橋護欄BG=1.8米,拉索AB與護欄的夾角是26°,拉索ED與護欄的夾角是60°,兩拉索底端距離BD為300m,若兩拉索頂端的距離AE為90m,請求出立柱AH的長.(tan26°≈0.5,sin26°≈0.4,![]() 1.7)
1.7)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com