Question

8．已知正方形ABCD和正方形CGEF，且D點在CF邊上，M為AE中點，連接MD、MF
（1）如圖1，請直接給出線段MD、MF的數量及位置關系是MD=MF，MD⊥MF；
（2）如圖2，把正方形CGEF繞點C順時針旋轉，則（1）中的結論是否成立？若成立，請證明；若不成立，請給出你的結論并證明；
（3）若將正方形CGEF繞點C順時針旋轉30°時，CF邊恰好平分線段AE，請直接寫出$\frac{CG}{CB}$的值．

Answer 1

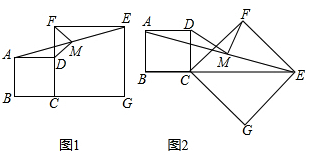
分析 （1）延長DM交EF于點P，易證AM=EM，即可證明△ADM≌△EPM，可得DM=PM，根據△DFP是直角三角形即可解題；
（2）延長DM交CE于點N，連接FN、DF，易證∠DAM=∠NEM，即可證明△ADM≌△ENM，可得EN=AD，DM=MN，可證CD=EN，即可證明△CDF≌△ENF，可得DF=NF，即可解題；
（3）根據（1）可得MD=MF，MD⊥MF，若CF邊恰好平分線段AE，則CF過點M，最后根據Rt△CDM中，∠DCF=30°，即可求得$\frac{CG}{CB}$的值．

解答 解：（1）線段MD、MF的數量及位置關系是MD=MF，MD⊥MF，
理由：如圖1，延長DM交EF于點P，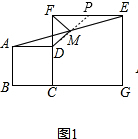

∵四邊形ABCD和四邊形FCGE是正方形，
∴AD∥EF，∠MAD=∠MEP．∠CFE=90°．
∴△DFP是直角三角形．
∵M為AE的中點，
∴AM=EM．
在△ADM和△EPM中，
$\left\{\begin{array}{l}{∠MAD=∠MEP}\\{AM=EM}\\{∠AMD=∠EMP}\end{array}\right.$，
∴△ADM≌△EPM（ASA），
∴DM=PM，AD=PE，
∴M是DP的中點．
∴MF=$\frac{1}{2}$DP=MD，
∵AD=CD，
∴CD=PE，
∵FC=FE，
∴FD=FP，
∴△DFP是等腰直角三角形，
∴FM⊥DP，即FM⊥DM．
故答案為：MD=MF，MD⊥MF；

（2）MD=MF，MD⊥MF仍成立．
證明：如圖2，延長DM交CE于點N，連接FN、DF，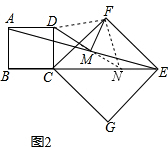

∵CE是正方形CFEG對角線，
∴∠FCN=∠CEF=45°，
∵∠DCE=90°，
∴∠DCF=45°，
∵AD∥BC，
∴∠DAM=∠NEM，
在△ADM和△ENM中，
$\left\{\begin{array}{l}{∠DAM=∠NEM}\\{AM=EM}\\{∠AMD=∠EMN}\end{array}\right.$，
∴△ADM≌△ENM（ASA），
∴EN=AD，DM=MN，
∵AD=CD，
∴CD=EN，
在△CDF和△ENF中，
$\left\{\begin{array}{l}{CD=EN}\\{∠DCF=∠CEF=45°}\\{CF=EF}\end{array}\right.$，
∴△CDF≌△ENF，（SAS）
∴DF=NF，
∴FM=DM，FM⊥DM．

（3）如圖所示，若CF邊恰好平分線段AE，則CF過點M，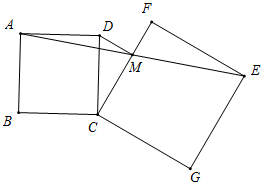

由（1）可得FM=DM，FM⊥DM，
設FM=DM=1，
∵∠DCF=30°，
∴Rt△DCM中，CM=$\sqrt{3}$，CD=2=CB，
∴CF=$\sqrt{3}$+1=CG，
∴$\frac{CG}{CB}$=$\frac{\sqrt{3}+1}{2}$．

點評 本題屬于四邊形綜合題，主要考查了全等三角形的判定，全等三角形對應邊相等的性質，含30°角的直角三角形的性質以及正方形的性質的綜合應用，本題中求證△ADM≌△ENM和△CDF≌△ENF是解題的關鍵．解題時注意：在直角三角形中，30°角所對的直角邊等于斜邊的一半．