
 已知二次函數的圖象與x軸有且只有一個交點A(-2,0),與y軸的交點為B(0,4),且其對稱軸與y軸平行.
已知二次函數的圖象與x軸有且只有一個交點A(-2,0),與y軸的交點為B(0,4),且其對稱軸與y軸平行.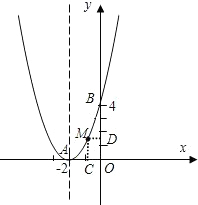
 )2+
)2+ ;
; 時,L有最小值
時,L有最小值 ,此時n=
,此時n= ;
; ,
, ).
).

科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
A、y=
| ||
B、y=-
| ||
C、y=-
| ||
D、y=
|
查看答案和解析>>
科目:初中數學 來源: 題型:
 已知二次函數的圖象與x軸交于點A(-1,0)和點B(3,0),且與直線y=kx-4交y軸于點C.
已知二次函數的圖象與x軸交于點A(-1,0)和點B(3,0),且與直線y=kx-4交y軸于點C. 查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com