
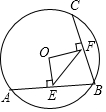
 如圖,在半徑為5的⊙O中,弦AB=8,點C是優弧$\widehat{AB}$上一點(不與A、B重合),OE⊥AB于E,OF⊥BC于F,求cos∠EFB的值.
如圖,在半徑為5的⊙O中,弦AB=8,點C是優弧$\widehat{AB}$上一點(不與A、B重合),OE⊥AB于E,OF⊥BC于F,求cos∠EFB的值. 分析 連接AC,作直徑BH,連接AH,根據垂徑定理和三角形中位線定理得到EF∥AC,根據勾股定理求出AH,根據余弦的定義計算即可.
解答 解: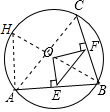 連接AC,作直徑BH,連接AH,
連接AC,作直徑BH,連接AH,
∵OE⊥AB于E,OF⊥BC于F,
∴BF=FC,BE=EA,
∴EF∥AC,
∴∠EFB=∠C,
∵BH為直徑,
∴∠HAB=90°,
∴AH=$\sqrt{B{H}^{2}-A{B}^{2}}$=6,
∴cos∠H=$\frac{HA}{BH}$=$\frac{6}{10}$=$\frac{3}{5}$,
∴cos∠EFB=$\frac{3}{5}$.
點評 本題考查的是垂直定理、圓周角定理、三角形的中位線定理,掌握垂直弦的直徑平分這條弦,并且平分弦所對的兩條弧是解題的關鍵.


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com