如圖，在等腰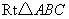
中，
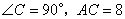，F是AB邊上的中點，點D、E分別在AC、BC邊上運動，且保持
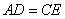．連接DE、DF、EF．在此運動變化的過程中，下列結論：①
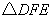是等腰直角三角形；②四邊形CDFE不可能為正方形，③DE長度的最小值為4；④四邊形CDFE的面積保持不變；⑤△CDE面積的最大值為8．其中正確的結論是（ ）
A．①④⑤ B．③④⑤ C．①③④ D．①②③
黃岡冠軍課課練系列答案科目：初中數學 來源： 題型：
如圖，設三角形ABC為一等腰直角三角形，角ABC為直角，D為AC中點。以B為圓心，AB為半徑作一圓弧AFC，以D為中心，AD為半徑，作一半圓AGC，作正方形BDCE。月牙形AGCFA的面積與正方形BDCE的面積大小關系（ ）
A、S月牙=S 正方形B、S月牙=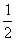
S 正方形 C、S月牙=
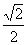S 正方形 D、S月牙=2S 正方形
查看答案和解析>>
科目：初中數學 來源： 題型：
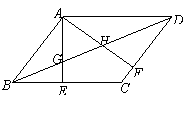
如圖，在□ABCD中，AE⊥BC于E，AF⊥CD于F，BD與AE、AF分別相交于G、H．
⑴求證：△ABE∽△ADF；
⑵若AG=AH，求證：四邊形ABCD是菱形．
查看答案和解析>>
科目：初中數學 來源： 題型：
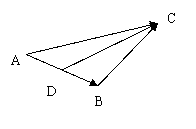
具有方向的線段叫做有向線段，以A為起點，B為終點的有向線段記作
，已知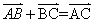
,如下圖所示：如果
，
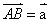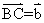，則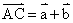
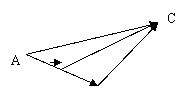
。若D為AB的中點，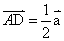
,若BE為AC上的中線，則用
,
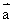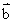表示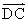
為__________________。
 |  | ||
查看答案和解析>>
科目：初中數學 來源： 題型：
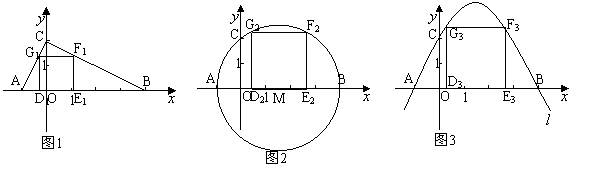
點A（-1,0）B（4,0）C（0,2）是平面直角坐標系上的三點。
① 如圖1先過A、B、C作△ABC，然后在在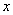
軸上方作一個正方形D1E1F1G1,
使D1E1在AB上， F1、G1分別在BC、AC上
② 如圖2先過A、B、C作圓⊙M，然后在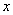軸上方作一個正方形D2E2F2G2,
使D2E2在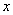軸上 ，F2、G2在圓上
③ 如圖3先過A、B、C作拋物線
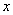，然后在軸上方作一個正方形D3E3F3G3,
使D3E3在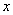軸上， F3、G3在拋物線上
請比較 正方形D1E1F1G1 , 正方形D2E2F2G2 , 正方形D3E3F3G3 的面積大小
查看答案和解析>>
科目：初中數學 來源： 題型：
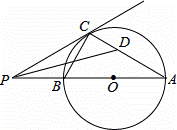
如圖，AB是⊙O的直徑，P為AB延長線上的一個動點，過點P作⊙O的切線，切點為C，連接AC，BC，作∠APC的平分線交AC于點D．
下列結論正確的是 （寫出所有正確結論的序號）
①△CPD∽△DPA；
②若∠A=30°，則P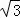C=
BC；
③若∠CPA=30°，則PB=OB；
④無論點P在AB延長線上的位置如何變化，∠CDP為定值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
上任意一點，則∠BEC 的度數為 （ ）
，若
隨
的值可以是（ ）