Question

13．如圖，在△ABC中，∠B=45°，∠C=30°，AB=8cm，求BC的長．（結果保留根號）

Answer 1

分析 過點A作AD⊥BC于D，得到兩個直角三角形，分別求出BD，CD的長即可得到BC的值．

解答 解：
過點A作AD⊥BC于D，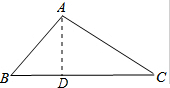
∵∠B=45°，
∴∠BAD=45°，
∴AD=BD，
∵AB=8cm，
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=4$\sqrt{2}$，
∵∠C=30°，
∴AD=$\frac{1}{2}$AC，
∴AC=8$\sqrt{2}$，
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=4$\sqrt{6}$，
∴BC=BD+CD=4$\sqrt{2}$+4$\sqrt{6}$．

點評 本題考查了勾股定理的運用，過點A作BC的垂線段，把△ABC分成兩個直角三角形是解題的關鍵．