
【題目】已知:直線EF分別與直線AB,CD相交于點F,E,EM平分∠FED,AB∥CD,H,P分別為直線AB和線段EF上的點。
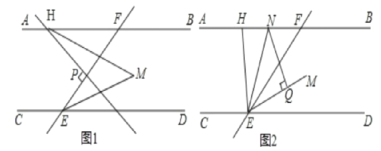
(1)如圖1,HM平分∠BHP,若HP⊥EF,求∠M的度數。
(2)如圖2,EN平分∠HEF交AB于點N,NQ⊥EM于點Q,當H在直線AB上運動(不與點F重合)時,探究∠FHE與∠ENQ的關系,并證明你的結論。
【答案】(1)45o (2)∠FHE=2∠ENQ或∠FHE=180°2∠ENQ,證明見解析
【解析】
(1)首先作MQ∥AB,根據平行線的性質,推得∠M=![]() (∠FHP+∠HFP);然后根據HP⊥EF,推得∠FHP+∠HFP=90°,據此求出∠M的度數即可.
(∠FHP+∠HFP);然后根據HP⊥EF,推得∠FHP+∠HFP=90°,據此求出∠M的度數即可.
(2)①如圖2,首先判斷出∠NEQ=∠NEF+∠QEF=![]() (∠HEF+∠DEF)=
(∠HEF+∠DEF)=![]() ∠HED,然后根據NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=
∠HED,然后根據NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=![]() (180°-∠HED)=
(180°-∠HED)=![]() ∠CEH,再根據AB∥CD,推得∠FHE=2∠ENQ即可.
∠CEH,再根據AB∥CD,推得∠FHE=2∠ENQ即可.
②如圖3,首先判斷出∠NEQ=∠QEF-∠NEF=![]() (∠DEF-∠HEF)=
(∠DEF-∠HEF)=![]() ∠HED,然后根據NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=
∠HED,然后根據NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=![]() (180°-∠HED)=
(180°-∠HED)=![]() ∠CEH,再根據AB∥CD,推得∠FHE=180°-2∠ENQ即可.
∠CEH,再根據AB∥CD,推得∠FHE=180°-2∠ENQ即可.
如圖1,作MQ∥AB,
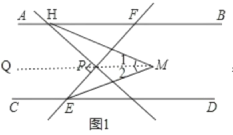
∵AB∥CD,MQ∥AB,
∴MQ∥CD,
∴∠1=∠FHM,∠2=∠DEM,
∴∠1+∠2=∠FHM+∠DEM=![]() (∠FHP+∠FED)=
(∠FHP+∠FED)= ![]() (∠FHP+∠HFP),
(∠FHP+∠HFP),
∵HP⊥EF,
∴∠HPF=90°,
∴∠FHP+∠HFP=180°90°=90°,
∵∠1+∠2=∠M,
∴∠M=![]() ×90°=45°.
×90°=45°.
(2)①如圖2,

∠FHE=2∠ENQ,理由如下:
∠NEQ=∠NEF+∠QEF=![]() (∠HEF+∠DEF)=
(∠HEF+∠DEF)= ![]() ∠HED,
∠HED,
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=![]() (180°∠HED)=
(180°∠HED)= ![]() ∠CEH,
∠CEH,
∵AB∥CD,
∴∠FHE=∠CEH=2∠ENQ.
②如圖3,

∠FHE=180°2∠ENQ,理由如下:
∠NEQ=∠QEF∠NEF=![]() (∠DEF∠HEF)=
(∠DEF∠HEF)= ![]() ∠HED,
∠HED,
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=![]() (180°∠HED)=
(180°∠HED)= ![]() ∠CEH,
∠CEH,
∵AB∥CD,
∴∠FHE=180°∠CEH=180°2∠ENQ.
綜上,可得當H在直線AB上運動(不與點F重合)時,∠FHE=2∠ENQ或∠FHE=180°2∠ENQ.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】由線段a,b,c組成的三角形不是直角三角形的是( )
A. a=15,b=8,c=17 B. a=12,b=14,c=15
C. a=![]() ,b=4,c=5 D. a=7,b=24,c=25
,b=4,c=5 D. a=7,b=24,c=25
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在□ABCD中,E、F分別是AB、CD的中點.
(1)求證:四邊形EBFD為平行四邊形;
(2)對角線AC分別與DE、BF交于點M、N.求證:△ABN≌△CDM.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,過點A(2,0)的兩條直線![]() ,
,![]() 分別交
分別交![]() 軸于B,C,其中點B在原點上方,點C在原點下方,已知AB=
軸于B,C,其中點B在原點上方,點C在原點下方,已知AB=![]() .
.

(1)求點B的坐標;
(2)若△ABC的面積為4,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠ACB=90°,BC=3cm,CD⊥AB,垂足為點D.在AC上取一點E,使EC=BC,過點E作EF⊥AC交CD的延長線于點F,若EF=7cm,則AE長為( ) .
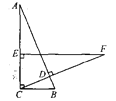
A.1cmB.2 cmC.3cmD.4cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,且AC在直線1上,將△ABC繞點A順時針旋轉到位置①,可得到點P1,將位置①的三角形繞點P1順時針旋轉到位置②,可得到點P2,將位置②的三角形繞點P2順時針旋轉到位置③,可得到點P3,…,按此規律繼續旋轉,得到點P2018為止,則AP2018=___.
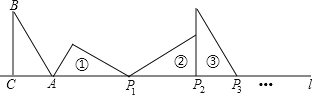
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在括號內填寫理由.
已知:如圖,DG⊥BC AC⊥BC,EF⊥AB,∠1=∠2.求證:CD⊥AB
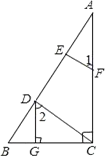
證明:∵DG⊥BC,AC⊥BC
∴∠DGB=∠ACB=90° ( )
∴DG∥AC( )
∴∠2=∠DCA ( )
∵∠1=∠2∴∠1=∠DCA
∴EF∥CD( )
∴∠AEF=∠ADC( )
∵EF⊥AB
∴∠AEF=90°
∴∠ADC=90° 即CD⊥AB.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,n+1個直角邊長為1的等腰直角三角形,斜邊在同一直線上,設△B2D1C1的面積為S1,△B3D2C2的面積為S2,…,△Bn+1DnCn的面積為Sn,則S1= ,Sn= (用含n的式子表示).
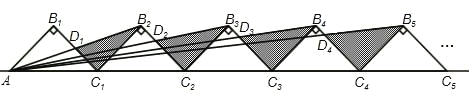
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com