【題目】在社會實踐活動中，某校甲、乙、丙三位同學一同調查了高峰時段北京的二環路、三環路、四環路的車流量(每小時通過觀測點的汽車車輛數)，三位匯報高峰時段的車流量情況如下：
甲同學說：“二環路車流量為每小時10000輛.”
乙同學說：“四環路比三環路車流量每小時多2000輛.”
丙同學說：“三環路車流量的3倍與四環路車流量的差是二環路車流量的2倍.”
請你根據他們提供的信息，求出高峰時段三環路、四環路的車流量各是多少？
科目：初中數學 來源： 題型：
【題目】某中學九年級數學興趣小組，在廣場上測量位于正東方向的某建筑物AC的高度，如圖所示，他先在點B測得該建筑物頂點A的仰角為30°，然后向正東方向前行62米，到達D點，再測得該建筑物頂點A的仰角為60°（B、C、D三點在同一水平面上，且測量儀的高度忽略不計）．求該建筑物AC的高度（結果精確的1米，參考數值：
）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小敏在研究數學問題時遇到一個定義：將三個已經排好順序數：x1，x2，x3，稱為數列x1，x2，x3．計算|x1|，
，
，將這三個數的最小值稱為數列x1，x2，x3的最佳值．例如，對于數列2，-1，3，因為|2|=2，
=
，
=
，所以數列2，-1，3的最佳值為．
小敏進一步發現：當改變這三個數的順序時，所得到的數列都可以按照上述方法計算其相應的最佳值．如數列-1，2，3的最佳值為；數列3，-1，2的最佳值為1；…．經過研究，小敏發現，對于“2，-1，3”這三個數，按照不同的排列順序得到的不同數列中，最佳值的最小值為．根據以上材料，回答下列問題：
（1）數列-4，-3，1的最佳值為______；
（2）將“-4，-3，2”這三個數按照不同的順序排列，可得到若干個數列，這些數列的最佳值的最小值為______，取得最佳值最小值的數列為______（寫出一個即可）；
（3）將2，-9，a（a＞1）這三個數按照不同的順序排列，可得到若干個數列．若這些數列的最佳值為1，求a的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】按照下列要求完成作圖及問題解答：
如圖，已知點A和線段BC.
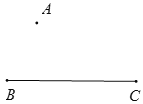
(1)連接AB；
(2)作射線CA；
(3)延長BC至點D，使得BD=2BC；
(4)通過測量可得∠ACD的度數是 ;
(5)畫∠ACD的平分線CE.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下面內容，并完成題目
通過計算容易得到下列算式: 
，
，
，...
（1）填寫計算結果
_ __, 
_ __, 
_ __，
（2）觀察以上各算式都是個位數字為5的數的平方數，可以看出規律，結果的末兩位數字都是25，即是原來數字個位數字5的平方，前面的數字就是原來的數去掉5以后的數字乘以比它大1的結果，如: 
就是
再連著寫25得到225，
就是
再連著寫25得到625，
就是
再連著寫25得到1225，...
如果記-一個個位數字是5的多位數為
,試用所學知識計算
并歸納解釋上述規律
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在□ABCD中，∠BAD，∠BCD的平分線分別交BC，AD于點F，E.
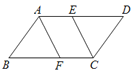
(1)求證：四邊形AFCE是平行四邊形；
(2)若BF=4，FC=3，求□ABCD的周長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，平行四邊形
中，
，
，
，點
與點
是平行四邊形邊上的動點，點以每秒
個單位長度的速度，從點
運動到點
，點以每秒
個單位長度的速度從點
→點
→點運動.當其中一個點到達終點時，另一個隨之停止運動.點與點同時出發，設運動時間為
，
的面積為
.
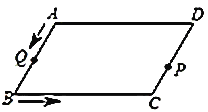
(1)求關于的函數關系式；
(2)為何值時，將以它的一邊為軸翻折，翻折前后的兩個三角形所組成的四邊形為菱形.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某小組6名同學參加一次知識競賽，共答20道題，每題分值相同，答對得分，答錯或不答扣分，下面是前5名同學的得分情況（如下表）：
（1）表中的m = ，n = ；
（2）該小組第6名同學說：“這次知識競賽我得了0分”，請問他的說法是否正確？如果正確，請求出這位同學答對了多少題；如果不正確，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
