
【題目】學習幾何的一個重要方法就是要學會抓住基本圖形,讓我們來做一次研究性學習.

(1)如圖①所示的圖形,像我們常見的學習用品一圓規,我們常把這樣的圖形叫做“規形圖”.請你觀察“規形圖”,試探究∠BOC與∠A、∠B、∠C之間的關系,并說明理由:
(2)如圖②,若△ABC中,BO平分∠ABC,CO平分∠ACB,且它們相交于點O,試探究∠BOC與∠A的關系;
(3)如圖③,若△ABC中,∠ABO=![]() ∠ABC,∠ACO=
∠ABC,∠ACO=![]() ∠ACB,且BO、CO相交于點O,請直接寫出∠BOC與∠A的關系式為 _.
∠ACB,且BO、CO相交于點O,請直接寫出∠BOC與∠A的關系式為 _.
【答案】(1)∠BOC=∠BAC+∠B+∠C.理由見解析;
(2)∠BOC=90°+![]() ∠A.理由見解析;
∠A.理由見解析;
(3)∠BOC=60°+![]() ∠A.理由見解析.
∠A.理由見解析.
【解析】
(1)如圖1,連接AO,延長AO到H.由三角形的外角的性質證明即可得到結論:∠BOC=∠BAC+∠B+∠C;
(2)利用角平分線的定義,三角形的內角和定理證明可得到結論:∠BOC=90°+![]() ∠A;
∠A;
(3)類似(2)可證明結論:∠BOC=60°+![]() ∠A.
∠A.
解:(1)∠BOC=∠BAC+∠B+∠C.
理由:
如圖1,連接AO,延長AO到H.
∵∠BOH=∠B+∠BAH,∠CAH=∠C+∠CAH,
∴∠BOC=∠B+∠BAH+∠CAH+∠C=∠BAC+∠B+∠C,
∴∠BOC=∠BAC+∠B+∠C;
(2)∠BOC=90°+![]() ∠A.
∠A.
理由:
如圖2,
∵OB,OC是△ABC的角平分線,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠BOC=180°-![]() (∠ABC+∠ACB)=180°-(180°-∠A)=90°+
(∠ABC+∠ACB)=180°-(180°-∠A)=90°+![]() ∠A,
∠A,
∴∠BOC=90°+![]() ∠A;
∠A;
(3)∠BOC=60°+![]() ∠A.
∠A.
理由:
∵∠ABO=![]() ∠ABC,∠ACO=
∠ABC,∠ACO=![]() ∠ACB,
∠ACB,
∴∠BOC=180°-![]() (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°-![]() (180°-∠A=60°+
(180°-∠A=60°+![]() ∠A.
∠A.
故答案為:∠BOC=60°+![]() ∠A.
∠A.


科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,E是邊AB上的一動點(不與點A、B重合),連接DE,點A關于直線DE的對稱點為F,連接EF并延長交BC于點G,連接DG,過點E作EH⊥DE交DG的延長線于點H,連接BH.
(1)求證:GF=GC;
(2)用等式表示線段BH與AE的數量關系,并證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,點D,E為⊙O上的兩個點,延長AD至C,使∠CBD=∠BED.
(1)求證:BC是⊙O的切線;
(2)當點E為弧AD的中點且∠BED=30°時,⊙O半徑為2,求DF的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一個半徑為r的圓形紙片在邊長為a( ![]() )的等邊三角形內任意運動,則在該等邊三角形內,這個圓形紙片“不能接觸到的部分”的面積是( )
)的等邊三角形內任意運動,則在該等邊三角形內,這個圓形紙片“不能接觸到的部分”的面積是( )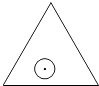
A.![]()
B.![]()
C.![]()
D.πr2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在8×8的正方形網格中,每個小正方形的邊長都為1個單位長度,△ABC的頂點都在正方形網格的格點上.
(1)將△ABC經平移后得到△A′B′C′,點A的對應點是點A′.畫出平移后所得的△A′B′C′;
(2)連接AA′、CC′,則四邊形AA′C′C的面積為 ________.
(3)若連接AA′,BB′,則這兩條線段之間的關系是 ;
(4)△ABC的高CD所在直線必經過圖中的一個格點點P,在圖中標出點P.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在每個小正方形邊長為1的方格紙中,△ABC的頂點都在方格紙格點上.
(1)△ABC的面積為 ;
(2)將△ABC經過平移后得到△A′B′C′,圖中標出了點B的對應點B',補全△A′B′C′;
(3)在圖中畫出△ABC的高CD;
(4)能使S△ABC=S△QBC的格點Q(A點除外)共有 個.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于x的方程 ![]() 有兩個不相等的實數根,
有兩個不相等的實數根,
(1)求m的取值范圍;
(2)是否存在實數m,使方程的兩個實數根的倒數和等于0?若存在,求出m的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水果店計劃進A,B兩種水果共140千克,這兩種水果的進價和售價如表所示
進價 | 售價 | |
A種水果 | 5 | 8 |
B種水果 | 9 | 13 |
![]() 若該水果店購進這兩種水果共花費1020元,求該水果店分別購進A,B兩種水果各多少千克?
若該水果店購進這兩種水果共花費1020元,求該水果店分別購進A,B兩種水果各多少千克?
![]() 在
在![]() 的基礎上,為了迎接春節的來臨,水果店老板決定把A種水果全部八折出售,B種水果全部降價
的基礎上,為了迎接春節的來臨,水果店老板決定把A種水果全部八折出售,B種水果全部降價![]() 出售,那么售完后共獲利多少元?
出售,那么售完后共獲利多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com