
【題目】小張在甲樓A處向外看,由于受到前面乙樓的遮擋,最近只能看到地面D處,俯角為α.小穎在甲樓B處(B在A的正下方)向外看,最近能看到地面E處,俯角為β,地面上G,F,D,E在同一直線上,已知乙樓高CF為10m,甲乙兩樓相距FG為15m,俯角α=45°,β=35°.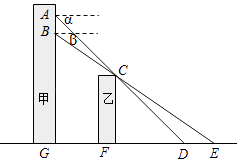
(1)求點A到地面的距離AG;
(2)求A,B之間的距離.(結果精確到0.1m)
(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
【答案】
(1)解:∵由已知得:∠AGD=∠BGE=∠CFD=90°,∠CDF=α=45°,
∴DF=CF=10,DG=FG+FD=15+10=25,
∴AG=GD=25,
答:位置A離地面的垂直距離為25米
(2)解:∵∠CEF=β=35°,
∴ ![]() =tan∠CEF=tan35°≈0.70,
=tan∠CEF=tan35°≈0.70,
∴EF= ![]() =
= ![]() ≈14.29,
≈14.29,
∴EG=GF+EF=15+14.29=29.29,
又∵ ![]() =tan∠CEF=tan35°≈0.70,
=tan∠CEF=tan35°≈0.70,
∴BG=0.70EG=0.70×29.29≈20.50,
∴AB≈25﹣20.50≈4.5.
答:A,B相差4.5米.
【解析】(1)先由等腰直角三角形的性質得出DF=CF,DG=FG+FD,進而可得出結論;(2)根據銳角三角函數的定義得出EF與BG的長,進而可得出結論.
【考點精析】利用關于仰角俯角問題對題目進行判斷即可得到答案,需要熟知仰角:視線在水平線上方的角;俯角:視線在水平線下方的角.


科目:初中數學 來源: 題型:
【題目】如圖,點E,F分別是矩形ABCD的邊BC和CD上的點,其中AB=3 ![]() ,BC=3
,BC=3 ![]() ,把△ABE沿AE進行折疊,使點B落在對角線AC上,在把△ADF沿AF折疊,使點D落在對角線AC上,點P為直線AF上任意一點,則PE的最小值為 .
,把△ABE沿AE進行折疊,使點B落在對角線AC上,在把△ADF沿AF折疊,使點D落在對角線AC上,點P為直線AF上任意一點,則PE的最小值為 . 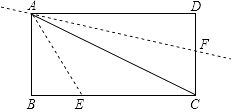
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠接受了20天內生產1200臺GH型電子產品的總任務.已知每臺GH型產品由4個G型裝置和3個H型裝置配套組成.工廠現有80名工人,每個工人每天能加工6個G型裝置或3個H型裝置.工廠將所有工人分成兩組同時開始加工,每組分別加工一種裝置,并要求每天加工的G、H型裝置數量正好全部配套組成GH型產品.
(1)按照這樣的生產方式,工廠每天能配套組成多少套GH型電子產品?請列出二元一次方程組解答此問題.
(2)為了在規定期限內完成總任務,工廠決定補充一些新工人,這些新工人只能獨立進行G型裝置的加工,且每人每天只能加工4個G型裝置.1.設原來每天安排x名工人生產G型裝置,后來補充m名新工人,求x的值(用含m的代數式表示)2.請問至少需要補充多少名新工人才能在規定期內完成總任務?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:三角形ABC內接于圓O,∠BAC與∠ABC的角平分線AE,BE相交于點E,延長AE交外接圓O于點D,連接BD,DC,且∠BCA=60°
(1)求∠BED的大小;
(2)證明:△BED為等邊三角形;
(3)若∠ADC=30°,圓O的半徑為r,求等邊三角形BED的邊長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一張寬為6cm的平行四邊形紙帶ABCD如圖1所示,AB=10cm,小明用這張紙帶將底面周長為10cm直三棱柱紙盒的側面進行包貼(要求包貼時沒有重疊部分).小明通過操作后發現此類包貼問題可將直三棱柱的側面展開進行分析.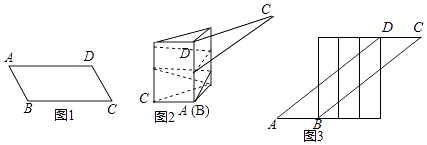
(1)若紙帶在側面纏繞三圈,正好將這個直三棱柱紙盒的側面全部包貼滿.則紙帶AD的長度為 cm;
(2)若AD=100cm,紙帶在側面纏繞多圈,正好將這個直三棱柱紙盒的側面全部包貼滿.則這個直三棱柱紙盒的高度是 cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AD∥BC,BE平分∠ABC交AD于點E,BD平分∠EBC.
(1)若∠DBC=30°,求∠A的度數;
(2)若點F在線段AE上,且7∠DBC-2∠ABF=180°,請問圖中是否存在與∠DFB相等的角?若存在,請寫出這個角,并說明理由;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD內有兩條相交線段MN,EF,M,N,E,F分別在邊AB,CD,AD,BC上.小明認為:若MN=EF,則MN⊥EF;小亮認為:若MN⊥EF,則MN=EF.你認為( )
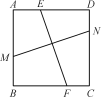
A. 僅小明對 B. 僅小亮對 C. 兩人都對 D. 兩人都不對
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分線EF交AC于點E,交BC于點F.試探索BF與CF的數量關系,寫出你的結論并證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB=AD,那么添加下列一個條件后,仍無法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com