
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 解:(1)設線段AB與y軸的交點為C,由拋物線的對稱性可得C為AB中點,
解:(1)設線段AB與y軸的交點為C,由拋物線的對稱性可得C為AB中點,| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AE |
| OE |
| OF |
| BF |
| 1 | ||
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| OF |
| BF |
| 1 | ||
|
| AE |
| OE |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AE |
| OF |
| OE |
| BF |
| 0.5m2 |
| n |
| m |
| 0.5n2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AE |
| OF |
| OE |
| BF |
| 0.5m2 |
| n |
| m |
| 0.5n2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |


 名師伴你成長課時同步學練測系列答案
名師伴你成長課時同步學練測系列答案科目:初中數學 來源: 題型:
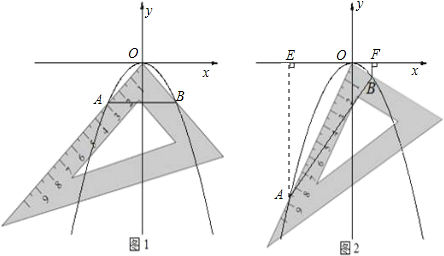
孔明是一個喜歡探究鉆研的同學,他在和同學們一起研究某條拋物線![]() 的性質時,將一把直角三角板的直角頂點置于平面直角坐標系的原點
的性質時,將一把直角三角板的直角頂點置于平面直角坐標系的原點![]() ,兩直角邊與該拋物線交于
,兩直角邊與該拋物線交于![]() 、
、![]() 兩點,請解答以下問題:
兩點,請解答以下問題:
(1)若測得![]() (如圖1),求
(如圖1),求![]() 的值;
的值;
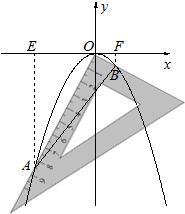
(2)對同一條拋物線,孔明將三角板繞點![]() 旋轉到如圖2所示位置時,過
旋轉到如圖2所示位置時,過![]() 作
作![]() 軸于點
軸于點![]() ,測得
,測得![]() ,寫出此時點
,寫出此時點![]() 的坐標,并求點
的坐標,并求點![]() 的橫坐標;
的橫坐標;
(3)對該拋物線,孔明將三角板繞點![]() 旋轉任意角度時驚奇地發現,交點
旋轉任意角度時驚奇地發現,交點![]() 、
、![]() 的連線段總經過一個固定的點,試說明理由并求出該點的坐標.
的連線段總經過一個固定的點,試說明理由并求出該點的坐標.
 |
查看答案和解析>>
科目:初中數學 來源:2012-2013學年浙江省溫州市瑞安市新紀元學校九年級(上)第一次月考數學試卷(解析版) 題型:解答題
 (如圖1),求a的值;
(如圖1),求a的值;
查看答案和解析>>
科目:初中數學 來源:2012年貴州省六盤水市中考數學模擬試卷(一)(解析版) 題型:解答題
 (如圖1),求a的值;
(如圖1),求a的值;
查看答案和解析>>
科目:初中數學 來源:2012年浙江省中考數學模擬試卷(五)(解析版) 題型:解答題
 (如圖1),求a的值;
(如圖1),求a的值;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com