Question

（2006•寧波）已知∠BAC=45°，一動點O在射線AB上運動（點O與點A不重合），設OA=x，如果半徑為1的⊙O與射線AC只有一個公共點，那么x的取值范圍是    ．

Answer 1

【答案】分析：如果半徑為1的⊙O與射線AC只有一個公共點，則有兩種情況，①當圓O與AC相切，連接圓心與切點的連線，由等腰直角三角形的性質求得OA的值；②當如圖位置時，OA小于圓的半徑，得到0＜x＜1．
解答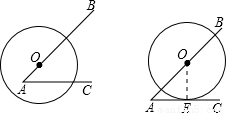：解：分兩種情況：
①如右圖，當圓O與AC相切時，圓O與AC只有一個公共點，設切點為E，連接OE
∴∠OAE=45°，
∵∠A=45°，
∴△OEA是等腰直角三角形，則
x=AO==；
②當為左圖時，點A在圓O內部時，圓O與AC只有一個公共點，此時OA小于圓O的半徑1，故有0＜x＜1．
點評：本題利用了切線的概念，等腰直角三角形的性質求解．