已知變量y與x成反比例,它的圖象過點A(-2,3).求:
(1)反比例函數解析式
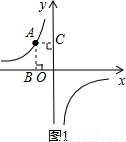
(2)從A(-2,3)向x軸和y軸分別作垂線AB、AC,垂足分別為B、C,則矩形OBAC的面積為______.
(3)當A點的橫坐標為-4時,作AB1、AC1分別垂直于x軸、y軸,B1、C1為垂足,則所得矩形OB1AC1的面積是______.
(4)將A點在圖象上任意移動到點A′,作A′B′、A′C′分別垂直于x軸、y軸,B′、C′為垂足,則所得矩形OB′A′C′的面積是______.
由此,你可以結合上述信息得出結論是:______.
【答案】
分析:(1)利用變量y與x成反比例,它的圖象過點A(-2,3),直接代入y=
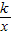
,求出即可;
(2)利用圖象上點的性質以及矩形面積求法得出即可;
(3)利用(2)中所求方法,即可得出矩形面積;
(4)利用以上面積求法即可得出矩形OB′A′C′的面積以及規律.
解答:解:(1)∵y與x成反比例,它的圖象過點A(-2,3),
代入y=
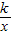
,∴k=xy=-6,
∴y=
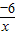
;
(2)如圖1:
∵從A(-2,3)向x軸和y軸分別作垂線AB、AC,垂足分別為B、C,
∴AC=2,AB=3,
∴矩形OBAC的面積為:2×3=6;
(3)如圖2,
∵A點的橫坐標為-4,
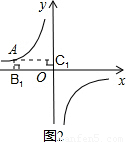
∴A點的縱坐標為:y=
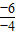
=

,
∴AB
1=

,AC
1=4,
∴矩形OB
1AC
1的面積是:4×

=6;
(4)同理可得出,A點在圖象上任意移動到點A′,作A′B′、A′C′分別垂直于x軸、y軸,B′、C′為垂足,
則所得矩形OB′A′C′的面積是:6,
∴反比例函數圖象上的點向坐標軸作垂線與坐標軸圍成的矩形的面積是定值,大小為|k|.
點評:此題主要考查了反比例函數的性質以及矩形面積求法,根據已知結合圖象得出是解題關鍵.

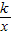 ,求出即可;
,求出即可;
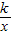 ,∴k=xy=-6,
,∴k=xy=-6,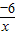 ;
;
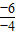 =
= ,
, ,AC1=4,
,AC1=4, =6;
=6;
