【題目】某化妝品銷售公司每月收益y萬元與銷售量x萬件的函數關系如圖所示．（收益=銷售利潤﹣固定開支）
（1）寫出圖中點A與點B的實際意義；
（2）求y與x的函數表達式；
（3）已知目前公司每月略有虧損，為了讓公司扭虧為盈，經理決定將每件產品的銷售單價提高2元，請在圖中畫出提價后y與x函數關系的圖象，并直接寫出該函數的表達式．（要標出確定函數圖象時所描的點的坐標）
世紀百通期末金卷系列答案科目：初中數學 來源： 題型：
【題目】為提高飲水質量，越來越多的居民開始選購家用凈水器．一商家抓住商機，從廠家購進了A、B兩種型號家用凈水器共160臺，A型號家用凈水器進價是150元/臺，B型號家用凈水器進價是350元/臺，購進兩種型號的家用凈水器共用去36000元．
（1）求A、B兩種型號家用凈水器各購進了多少臺；
（2）為使每臺B型號家用凈水器的毛利潤是A型號的2倍，且保證售完這160臺家用凈水器的毛利潤不低于11000元，求每臺A型號家用凈水器的售價至少是多少元？（注：毛利潤=售價﹣進價）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】把一副三角板如圖甲放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜邊AB=12，DC=14，把三角板DCE繞點C順時針旋轉15°得到△D1CE1（如圖乙），此時AB與 CD1交于點O，則線段AD1的長為（ ）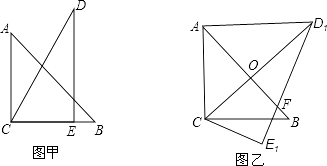 
A.6 
B.10
C.8
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】出租車司機小李某天下午運營全是在東西走向的人民大道上進行的，如果規定向東為正，向西為負，他這天下午行駛里程如下：（單位：千米）
+15, -3, +14，-11，+10，-12，+4，-15，+16，-18
（1）他將最后一名乘客送到目的地時，距下午出車地點是多少千米？
（2）若汽車耗油量為
升∕千米，這天下午共耗油多少升
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】綜合題
（1）已知二次函數y=ax2+bx+1的圖象經過點（1，3）和（3，﹣5），求a、b的值；
（2）已知二次函數y=﹣x2+bx+c的圖象與x軸的兩個交點的橫坐標分別為1和2．求這個二次函數的表達式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，DG⊥BC，AC⊥BC，EF⊥AB，∠1=∠2，求證：CD⊥AB．
證明：∵DG⊥BC，AC⊥BC（已知）
∴∠DGB=∠ACB=90°（垂直定義）
∴DG∥AC（ ）
∴∠2= （ ）
∵∠1=∠2（已知）
∴∠1=∠ （等量代換）
∴EF∥CD（ ）
∴∠AEF=∠ （ ）
∵EF⊥AB（已知）
∴∠AEF=90°（ ）
∴∠ADC=90°（ ）
∴CD⊥AB（ ）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知直線l1∥l2，A，B分別是l1，l2上的點，l3和l1，l2分別交于點C，D，P是線段CD上的動點(點P不與C，D重合)．
(1)若∠1＝150°，∠2＝45°，求∠3的度數；
(2)若∠1＝α，∠2＝β，用α，β表示∠APC＋∠BPD.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖①已知正方形ABCD的邊BC、CD上分別有E、F兩點，且∠EAF=45°，現將△ADF繞點A順時針旋轉90°至△ABH處.
（1）線段EF、BE、DF有何數量關系？并說明理由；
模仿（1）中的方法解決（2）、（3）兩個問題：
（2）如圖②，若將E、F移至BD上，其余條件不變，且BE=
，DF=3，求EF的長；
（3）如圖③，圖形變成矩形ABCD，∠EAF=45°，BE=3，AB=6，AD=10，求DF和EF的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，將坐標原點O沿x軸向左平移2個單位長度得到點A，過點A作y軸的平行線交反比例函數
的圖象于點B，AB=
．
（1）求反比例函數的解析式；
（2）若P（
， 
）、Q（
， 
）是該反比例函數圖象上的兩點，且
時， 
，指出點P、Q各位于哪個象限？并簡要說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
