
【題目】如圖①已知正方形ABCD的邊BC、CD上分別有E、F兩點,且∠EAF=45°,現將△ADF繞點A順時針旋轉90°至△ABH處.
(1)線段EF、BE、DF有何數量關系?并說明理由;
模仿(1)中的方法解決(2)、(3)兩個問題:
(2)如圖②,若將E、F移至BD上,其余條件不變,且BE=![]() ,DF=3,求EF的長;
,DF=3,求EF的長;
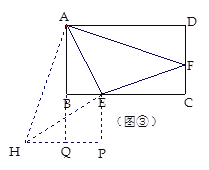
(3)如圖③,圖形變成矩形ABCD,∠EAF=45°,BE=3,AB=6,AD=10,求DF和EF的長.

【答案】(1) EF=BE+DF;(2) ![]() ;(3)
;(3) ![]() ,
,![]() .
.
【解析】試題分析:(1)由旋轉的性質得:△ADF≌△ABH,從而可由SAS證△HAE≌△FAE,得到EF=HE,從而得到結論;
(2)把△ABE繞點A旋轉90°到△ADG,連接GF.同(1)可得:△AGD≌△AEB,△AEF≌△AGF,得到BE=GD,∠GDA=∠EBA=45°,EF=GF,由∠FDA=45°,得到∠FDG=90°.在Rt△GDF中,由勾股定理即可得到結論;
(3)把△ADF繞A旋轉90°到△AQH,連接EH,過E作EP⊥HQ 于P.同理得△ADF≌△AQH,△HAE≌△FAE,EF=HE.設DF=x.在Rt△HPE與Rt△ECF中,由勾股定理即可得出結論.
試題解析:解:(1)EF=BE+DF.理由如下:
由旋轉的性質得:△ADF≌△ABH,∴AH=AF,DF=HB,∠HAB=∠DAF.∵∠DAF+∠FAB=90°,∴∠FAH=90°.∵∠EAF=45°,∴∠EAH=45°,∴∠EAF=∠EAH.在△EAF和△EAH中,∵AF=AH,∠EAF=∠HAE,AE=AE,∴△HAE≌△FAE(SAS),∴EF=HE.∵HE=HB+BE=DF+BE,∴EF=BE+DF;
(2)把△ABE繞點A旋轉90°到△ADG,連接GF.同(1)可得:△AGD≌△AEB,△AEF≌△AGF,∴BE=GD,∠GDA=∠EBA=45°,EF=GF.∵∠FDA=45°,∴∠FDG=90°,∴EF=FG=![]() =
=![]() =
=![]() =
=![]() ;
;

(3)把△ADF繞A旋轉90°到△AQH,連接EH,過E作EP⊥HQ 于P.
同理得△ADF≌△AQH,△HAE≌△FAE(SAS),∴EF=HE.
設DF=x.在Rt△HPE與Rt△ECF中,由勾股定理得:
![]() ,
,![]()
∴![]()
![]() ;
;
解得:![]()
![]() ,∴DF=
,∴DF=![]() ,EF=
,EF=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】(1)算一算下面兩組算式:(3×5)2與32×52;[(-2)×3]2與(-2)2×32,每組兩個算式的結果是否相同?
(2)想一想,(a×b)3等于什么?
(3)猜一猜,當n為正整數時,(a×b)n等于什么?你能利用乘方的意義說明理由嗎?
(4)利用上述結論,計算:(-8)2018×(0.125)2019.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某化妝品銷售公司每月收益y萬元與銷售量x萬件的函數關系如圖所示.(收益=銷售利潤﹣固定開支)
(1)寫出圖中點A與點B的實際意義;
(2)求y與x的函數表達式;
(3)已知目前公司每月略有虧損,為了讓公司扭虧為盈,經理決定將每件產品的銷售單價提高2元,請在圖中畫出提價后y與x函數關系的圖象,并直接寫出該函數的表達式.(要標出確定函數圖象時所描的點的坐標)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學習有理數的乘法后,老師給同學們這樣一道題目:計算:49![]() ×(﹣5),看誰算的又快又對,有兩位同學的解法如下:
×(﹣5),看誰算的又快又對,有兩位同學的解法如下:
小明:原式=﹣![]() ×5=﹣
×5=﹣![]() =﹣249
=﹣249![]() ;
;
小軍:原式=(49+![]() )×(﹣5)=49×(﹣5)+
)×(﹣5)=49×(﹣5)+![]() ×(﹣5)=﹣249
×(﹣5)=﹣249![]() ;
;
(1)對于以上兩種解法,你認為誰的解法較好?
(2)上面的解法對你有何啟發,你認為還有更好的方法嗎?如果有,請把它寫出來;
(3)用你認為最合適的方法計算:19![]() ×(﹣8)
×(﹣8)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】市射擊隊為從甲、乙兩名運動員中選拔一人參加省比賽,對他們進行了六次測試,測試成績如表(單位:環):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根據表格中的數據,分別計算甲、乙的平均成績;
(2)已知甲六次成績的方差S甲2= ![]() ,試計算乙六次測試成績的方差;根據(1)、(2)計算的結果,你認為推薦誰參加省比賽更合適,請說明理由.
,試計算乙六次測試成績的方差;根據(1)、(2)計算的結果,你認為推薦誰參加省比賽更合適,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)(-3)-(-15)÷(-3); (2)(-42)÷(-7)-(-6)×4;
(3)-14-![]() ×[2-(-3)2]; (4)-13-(1-0.5)2×
×[2-(-3)2]; (4)-13-(1-0.5)2×![]() ×(2-22);
×(2-22);
(5)10+8×(-![]() )2-2÷
)2-2÷![]() ; (6)(-1)10-(-3)×|
; (6)(-1)10-(-3)×|![]() -
-![]() |÷
|÷![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中:A(1,1),B(-1,1),C(-1,-2),D(1,-2),現把一條長為2 018個單位長度且沒有彈性的細線(線的粗細忽略不計)的一端固定在點A處,并按A→B→C→D→A→…的規律緊繞在四邊形ABCD的邊上,則細線另一端所在位置的點的坐標是________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據要求,解答下列問題:
(1)解答下列問題 ①方程x2﹣2x+1=0的解為;
②方程x2﹣3x+2=0的解為;
③方程x2﹣4x+3=0的解為;
…
(2)根據以上方程特征及其解的特征,請猜想: ①方程x2﹣9x+8=0的解為;
②關于x的方程的解為x1=1,x2=n.
(3)請用配方法解方程x2﹣9x+8=0,以驗證猜想結論的正確性.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知E是正方形ABCD的邊CD外的一點,△DCE為等邊三角形,BE交對角線AC于F .
(1)求∠AFD的度數;
(2)求證:AF = EF.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com