
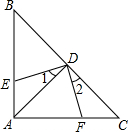
 如圖,△ABC中,∠BAC=90°,AB=AC,點D是斜邊BC的中點,DE⊥DF,若AB=8cm,則四邊形AEDF的面積為( )
如圖,△ABC中,∠BAC=90°,AB=AC,點D是斜邊BC的中點,DE⊥DF,若AB=8cm,則四邊形AEDF的面積為( )| A. | 64 | B. | 32 | C. | 16 | D. | 8 |
分析 利用點D是斜邊BC的中點,可以得到AD⊥BC,而DE⊥DF,得出∠1=∠2;由等腰直角三角形ABC的性質及∠1=∠2可以證明△ADE≌△CDF;得出S△ADE=S△CDF,得到S四邊形AEDF=S△ADE+S△ADF=S△CDF+S△ADF=S△ACD=$\frac{1}{2}$S△ABC,即可得出結果.
解答 解:∵AB=AC,點D是BC中點,
∴AD⊥BC.
∴∠2=90°-∠ADF.
∵DE⊥DF,
∴∠1=90°-∠ADF.
∴∠1=∠2.
∵AB=AC,∠BAC=90°,
∴∠C=45°.
又∵點D是BC中點,
∴∠DAC=∠EAD=$\frac{1}{2}$∠BAC=45°.
∴∠C=∠EAD=∠DAC.
∴AD=CD.
在△ADE和△CDF中,$\left\{\begin{array}{l}{∠1=∠2}&{\;}\\{AD=CD}&{\;}\\{∠EAD=∠C}&{\;}\end{array}\right.$,
∴△ADE≌△CDF(ASA).
∴S△ADE=S△CDF,
∴S四邊形AEDF=S△ADE+S△ADF=S△CDF+S△ADF
=S△ACD=$\frac{1}{2}$S△ABC
=$\frac{1}{2}$×$\frac{1}{2}$×8×8=16cm2.
故選:C.
點評 此題主要考查了等腰直角三角形的性質、全等三角形的判定與性質;熟練掌握等腰直角三角形的性質,證明三角形全等是解決問題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 名稱 | 三棱柱 | 四棱柱 | 五棱柱 | 六棱柱 |
| 圖形 |  |  |  | 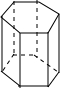 |
| 頂點數a | 6 | 8 | 10 | 12 |
| 棱數b | 9 | 12 | 15 | 18 |
| 面數c | 5 | 6 | 7 | 8 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
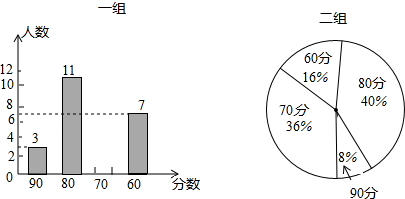
| 平均數 | 中位數 | 眾數 | 方差 | |
| 一組 | 74 | 80 | 80 | 104 |
| 二組 | 74 | 70 | 80 | 72 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
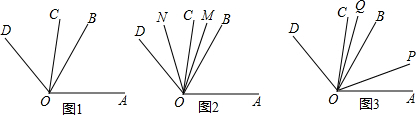
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com