
【題目】綜合與實踐
問題情境:在數學課上,老師呈現了這樣一個問題:
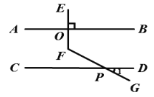
如圖,已知![]() ,
,![]() 于點
于點![]() ,
,![]() 交
交![]() 于點
于點![]() ,當
,當![]() 時,求
時,求![]() 的度數.
的度數.
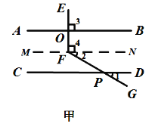
交流分享:勤思組的甲、乙、丙三位同學通過添加不同的輔助線均解決了問題,如下圖:
合作提升:完成下列問題:
(1)請根據甲同學的圖形,完成下列推理過程:
解:過點![]() 作
作![]()
∴![]() __________
__________![]() ( )
( )
∵![]()
∴![]() ( )
( )
∵![]()
![]()
∴![]() ( )
( )
∴![]()
∴![]() ___________=___________°
___________=___________°
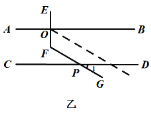
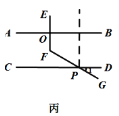
(2)請仔細觀察乙、丙兩位同學所畫圖形,選擇其中一個,求![]() 的度數.
的度數.
【答案】(1)2;兩直線平行,同位角相等;垂直的定義,平行于同一條直線的兩直線平行;2;120;(2)見解析
【解析】
(1)過F作MN∥CD,根據平行線的性質以及垂線的定義,即可得到∠EFG的度數;
(2)選擇丙,過P作PN∥EF,根據平行線的性質,可得∠NPD的度數,再根據∠1的度數以及平行線的性質,即可得到∠EFG的度數;
(1)過點![]() 作
作![]() ,
,

∴![]()
![]()
![]() (兩直線平行,同位角相等),
(兩直線平行,同位角相等),
∵![]() ,
,
∴![]() (垂直的定義),
(垂直的定義),
∵![]() ,
, ![]() ,
,
∴![]() ( 平行于同一條直線的兩直線平行 ),
( 平行于同一條直線的兩直線平行 ),
∴![]() ,
,
∴![]() 2=120°
2=120°
故答案為:2;兩直線平行,同位角相等;垂直的定義;平行于同一條直線的兩直線平行;2;120;
(2)選擇丙,理由如下:
如圖丙,過P作PN∥EF,
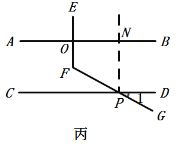
∵PN∥EF,EF⊥AB,
∴∠ONP=∠EOB=90°,
∵AB∥CD,
∴∠NPD=∠ONP=90°,
又∵∠1=30°,
∴∠NPG=90°+30°=120°,
∵PN∥EF,
∴∠EFG=∠NPG=120°;


科目:初中數學 來源: 題型:
【題目】某校以“我最想去的社會實踐地”為課題,開展了一次調查,從全校同學中隨機抽取了部分同學進行調查,每位同學從“蓀湖花海”、“保國寺”、“慈城古鎮”、“綠色學校”中選取一項最想去的社會實踐地,并將調查結果繪制成如下的統計圖(部分信息未給出).

請根據統計圖中信息,解答下列問題:
(1)該調查的樣本容量為________,a=________%,b=________%,“蓀湖花海”所對應扇形的圓心角度數為________度.
(2)補全條形統計圖;
(3)若該校共有1600名學生,請估計全校最想去“綠色學校”的學生共有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小剛同學動手剪了如圖①所示![]() ,
,![]() 的正方形紙片與
的正方形紙片與![]() 的長方形紙片若干塊.
的長方形紙片若干塊.
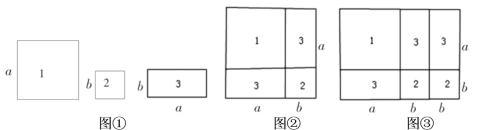
(1)小剛用1張1號、1張2號和2張3號紙片拼出一個新圖形(如圖②),根據這個圖形的面積關系可以寫出一個你所熟悉的乘法公式,這個乘法公式是 ;
(2)根據小剛用1張1號、2張2號和3張3號紙片拼成的長方形(如圖③),6張紙片的面積等于所拼成大長方形的面積,將多項式![]() 因式分解,其結果是 ;
因式分解,其結果是 ;
(3)動手操作,請你依照小剛的方法,利用拼圖分解因式:![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD是平行四邊形,小慧同學利用直尺和規進行了如下操作:①連接AC,分別以點A、C為圓心,以大于![]() AC的長為半徑畫弧,兩弧相交于點P、Q;②作直線PQ,分別交BC、AC、AD于點E、O、F,連接AE、CF.根據操作結果,解答下列問題:
AC的長為半徑畫弧,兩弧相交于點P、Q;②作直線PQ,分別交BC、AC、AD于點E、O、F,連接AE、CF.根據操作結果,解答下列問題:
(1)線段AF與CF的數量關系是 .
(2)若∠BAD=120°,AE平分∠BAD,AB=8,求四邊形AECF的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每年5月20日是中國學生營養日,按時吃早餐是一種健康的飲食習慣.為了解本校七年級學生飲食習慣,李明和同學們在七年級隨機調查了一部分學生每天吃早餐的情況,并將統計結果繪制成如下統計圖(不完整).圖中![]() 表示不吃早餐,
表示不吃早餐,![]() 表示偶爾吃早餐,
表示偶爾吃早餐,![]() 表示經常吃早餐,
表示經常吃早餐,![]() 表示每天吃早餐.請根據統計圖解答以下問題:
表示每天吃早餐.請根據統計圖解答以下問題:
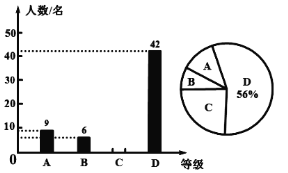
(1)這次共調查了多少名學生?
(2)請補全條形統計圖;
(3)這個學校七年級共有學生1200名,請估計這個學校七年級每天約有多少名學生不吃早餐?
(4)請根據此次調查結果提一條合理的建議。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)下面兩個立體圖形的名稱是:__________,__________
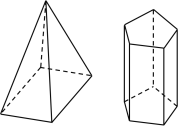
(2)一個立體圖形的三視圖如下圖所示,這個立體圖形的名稱是__________

(3)畫出下面立體圖形的主視圖.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為實施“農村留守兒童關愛計劃”,某校結全校各班留守兒童的人數情況進行了統計,發現各班留守兒童人數只有1名、2名、3名、4名、5名、6名共六種情況,并制成如下兩幅不完整的統計圖:
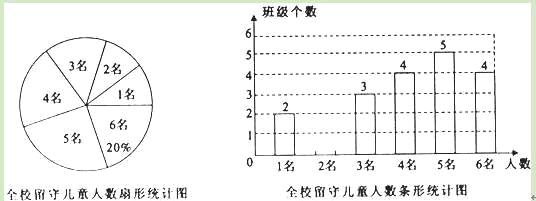
(1)求該校平均每班有多少名留守兒童?并將該條形統計圖補充完整;
(2)某愛心人士決定從只有2名留守兒童的這些班級中,任選兩名進行生活資助,請用列表法或畫樹狀圖的方法,求出所選兩名留守兒童來自同一個班級的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,AB∥CD,點P為定點,E、F分別是AB、CD上的動點.
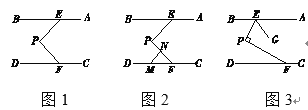
(1)求證:∠P=∠BEP+∠PFD;
(2)若點M為CD上一點,如圖2,∠FMN=∠BEP,且MN交PF于N.試說明∠EPF與∠PNM的數量關系,并證明你的結論;
(3)移動E、F使得∠EPF=90°,如圖3,作∠PEG=∠BEP,求∠AEG與∠PFD度數的比值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市開展“美麗自宮,創衛同行”活動,某校倡議學生利用雙休日在“花海”參加義務勞動,為了解同學們勞動情況,學校隨機調查了部分同學的勞動時間,并用得到的數據繪制了不完整的統計圖,根據圖中信息回答下列問題:
(1)將條形統計圖補充完整;
(2)扇形圖中的“1.5小時”部分圓心角是多少度?
(3)求抽查的學生勞動時間的眾數、中位數.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com