【題目】每年5月20日是中國學生營養日，按時吃早餐是一種健康的飲食習慣．為了解本校七年級學生飲食習慣，李明和同學們在七年級隨機調查了一部分學生每天吃早餐的情況，并將統計結果繪制成如下統計圖（不完整）．圖中
表示不吃早餐，
表示偶爾吃早餐，
表示經常吃早餐，
表示每天吃早餐．請根據統計圖解答以下問題：
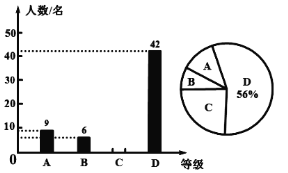
（1）這次共調查了多少名學生？
（2）請補全條形統計圖；
（3）這個學校七年級共有學生1200名，請估計這個學校七年級每天約有多少名學生不吃早餐？
（4）請根據此次調查結果提一條合理的建議。
【答案】（1）這次共調查了75名學生；（2）見解析；（3）這個學校七年級每天約有144名學生不吃早餐．；（4）見解析
【解析】
（1）抽查人數可由D等級的人數42及所占的比例為56%，根據總數=某等人數÷比例來計算；
（2）用抽取的總人數減去其他等級的人數得到C等級的人數，從而補全統計圖；
（3）用總人數乘以樣本中A等級的百分比即可得；
（4）根據題意給出合理建議均可．
（1）∵D的人數為42及所占的比例為56%，
∴
（名），
答：這次共調查了75名學生；
（2）C的人數為：
（名），
補全條形圖如下：
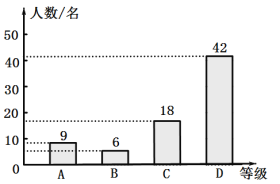
（3）學校1200名七年級學生每天不吃早餐人數為：
（名），
答：這個學校七年級每天約有144名學生不吃早餐；
（4）建議同學們每天吃早餐（答案不唯一）．
科目：初中數學 來源： 題型：
【題目】點 O 是直線 AB上一點，∠COD 是直角，OE平分∠BOC．
（1）①如圖1，若∠DOE＝25°，求∠AOC 的度數；
②如圖2，若∠DOE＝α，直接寫出∠AOC的度數（用含α的式子表示）；
（2）將圖 1中的∠COD 繞點O按順時針方向旋轉至圖 2 所示位置．探究∠DOE 與∠AOC 的度數之間的關系，寫出你的結論，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,AM是△ABC的中線,D是線段AM上一點(不與點A重合)DE∥AB交AC于點F,CE∥AM,連結AE.
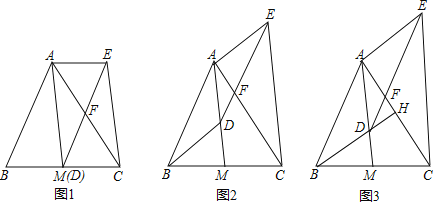
(1)如圖1,當點D與M重合時,求證:四邊形ABDE是平行四邊形;
(2)如圖2,當點D不與M重合時,(1)中的結論還成立嗎?請說明理由.
(3)如圖3,延長BD交AC于點H,若BH⊥AC,且BH=AM
①求∠CAM的度數;
②當FH=
, DM=4時,求DH的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】蕭山北干初中組織外國教師（外教）進班上英語課，王明同學為了解全校學生對外教的喜愛程度，在全校隨機抽取了若干名學生進行問卷調查．問卷將喜愛程度分為A（非常喜歡）、B（喜歡）、C（不太喜歡）、D（很不喜歡）四種類型，根據調查結果繪制成了兩幅不完整的統計圖，請結合統計圖信息解答下列問題：
（1）這次調查中，一共調查了 名學生，圖1中C類所對應的圓心角度數為 ；
（2）請補全條形統計圖；
（3）在非常喜歡外教的5位同學（三男兩女）中任意抽取兩位同學作為交換生，請用列表法或畫樹狀圖求出恰好抽到一名男生和一名女生作為交換生的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】長江中下游地區特大旱情發生后，全國人民抗旱救災，眾志成城．市政府籌集了抗旱必需物資120噸打算運往災區，現有甲、乙、丙三種車型供選擇，每輛車的運載能力和運費如下表所示：（假設每輛車均滿載）
車型 | 甲 | 乙 | 丙 |
汽車運載量（噸/輛） | 5 | 8 | 10 |
汽車運費（元/輛） | 400 | 500 | 600 |
（1）若全部物資都用甲、乙兩種車型來運送，需運費8200元，問分別需甲、乙兩種車型各幾輛？
（2）為了節省運費，溫州市政府打算用甲、乙、丙三種車型同時參與運送，已知它們的總輛數為14輛，你能分別求出三種車型的輛數嗎？此時的運費又是多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】綜合與實踐
問題情境：在數學課上，老師呈現了這樣一個問題：
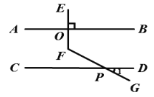
如圖，已知
，
于點
，
交
于點
，當
時，求
的度數．
交流分享：勤思組的甲、乙、丙三位同學通過添加不同的輔助線均解決了問題，如下圖：
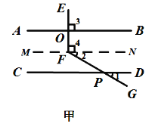
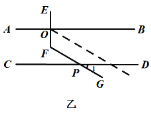
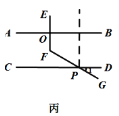
合作提升：完成下列問題：
（1）請根據甲同學的圖形，完成下列推理過程：
解：過點
作
∴
__________
( )
∵
∴
（ ）
∵
∴
( )
∴
∴
___________=___________°
（2）請仔細觀察乙、丙兩位同學所畫圖形，選擇其中一個，求的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】杰瑞公司成立之初投資1500萬元購買新生產線生產新產品，此外，生產每件該產品還需要成本60元.按規定，該產品售價不得低于100元/件且不得超過180元/件，該產品銷售量y（萬件）與產品售價x（元）之間的函數關系如圖所示.
(1)求y與x之間的函數關系式，并寫出x的取值范圍；
(2)第一年公司是盈利還是虧損？求出當盈利最大或者虧損最小時的產品售價；
(3)在(2)的前提下，即在第一年盈利最大或者虧損最小時，第二年公司重新確定產品售價，能否使兩年共盈利達1340萬元，若能，求出第二年產品售價；若不能，請說明理由.
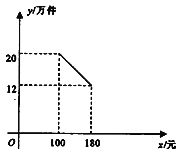
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖：數軸上有
、
兩點，分別對應的數為
，
，已知
與
互為相反數，點
為數軸上一動點，對應為
．
(1)若點到點和點的距離相等，求點對應的數；
(2)數軸上是否存在點，使點到點和點的距離之和為5?若存在，請求出的值，若不存在，請說明理由；
(3)當點以每分鐘1個單位長度的速度從
點向左運動，點以每分鐘5個單位長度向左運動，點以每分鐘20個單位長度的速度向左運動，問幾分鐘時點到點、點的距離相等．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
