
【題目】已知Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°.
(1)將這兩個三角形按圖①方式擺放,使點E落在AB上,DE的延長線交BC于點F.求證:BF+EF=DE;
(2)改變△ADE的位置,使DE交BC的延長線于點F(如圖②),則(1)中的結論還成立嗎?若成立,加以證明;若不成立,寫出此時BF、EF與DE之間的等量關系,并說明理由.

【答案】(1)證明見解析;(2) (1)中的結論不成立,有DE=BF﹣EF,理由見解析.
【解析】試題分析:(1)由Rt△ABC≌Rt△ADE得AC=AE,根據HL可證得Rt△ACF≌Rt△AEF,由BC=BF+CF代入可得結論;
(2)如圖②,(1)中的結論不成立,有DE=BF-EF,同(1):證明Rt△ACF≌Rt△AEF,再由BC=BF-FC得出結論.
試題解析:(1)如圖①,連接AF,
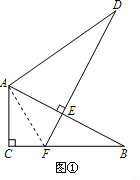
∵Rt△ABC≌Rt△ADE,
∴AC=AE,BC=DE,
∵∠ACB=∠AEF=90°,AF=AF,
∴Rt△ACF≌Rt△AEF,
∴CF=EF,
∴BF+EF=BF+CF=BC,
∴BF+EF=DE;
(2)如圖②,(1)中的結論不成立,有DE=BF-EF,理由是:
連接AF,

∵Rt△ABC≌Rt△ADE,
∴AC=AE,BC=DE,
∵∠E=∠ACF=90°,AF=AF,
∴Rt△ACF≌Rt△AEF,
∴CF=EF,
∴DE=BC=BF-FC=BF-EF,
即DE=BF-EF.


 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:初中數學 來源: 題型:
【題目】“校園安全”受到全社會的廣泛關注,東營市某中學對部分學生就校園安全知識的了解程度,采用隨機抽樣調查的方式,并根據收集到的信息進行統計,繪制了下面兩幅尚不完整的統計圖.請你根據統計圖中所提供的信息解答下列問題:
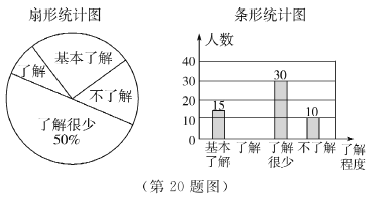
(1)接受問卷調查的學生共有_______人,扇形統計圖中“基本了解”部分所對應扇形的圓心角為_______°;
(2)請補全條形統計圖;
(3)若該中學共有學生900人,請根據上述調查結果,估計該中學學生中對校園安全知識達到“了解”和“基本了解”程度的總人數;
(4)若從對校園安全知識達到“了解”程度的3個女生和2個男生中隨機抽取2人參加校園安全知識競賽,請用樹狀圖或列表法求出恰好抽到1個男生和1個女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為了解學生對新聞、體育、動畫、娛樂、戲曲五類電視節目最喜愛的情況,隨機調查了若干名學生,根據調查數據進行整理,繪制了如下的不完整統計圖:

請你根據以上的信息,回答下列問題:
(1) 本次共調查了_____名學生,其中最喜愛戲曲的有_____人;在扇形統計圖中,最喜愛體育的對應扇形的圓心角大小是______;
(2) 根據以上統計分析,估計該校2000名學生中最喜愛新聞的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
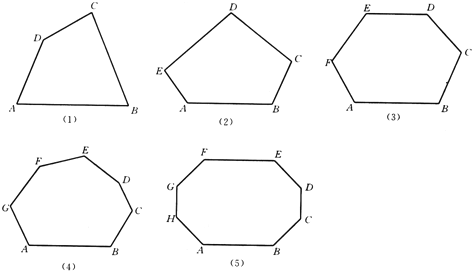
【題目】分別畫出下列各多邊形的對角線,并觀察圖形完成下列問題:
(1)試寫出用n邊形的邊數n表示對角線總條數S的式子: .
(2)從十五邊形的一個頂點可以引出 條對角線,十五邊形共有 條對角線:
(3)如果一個多邊形對角線的條數與它的邊數相等,求這個多邊形的邊數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了測量校園水平地面上一棵樹的高度,數學興趣小組利用一根標桿、皮尺,設計如圖所示的測量方案.已知測量同學眼睛A、標桿頂端F、樹的頂端E在同一直線上,此同學眼睛距地面1.6米,標桿高為3.2米,且BC=2米,CD=6米,求樹ED的高.
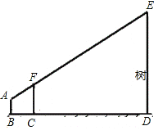
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點P在第四象限,且到x軸的距離為4,到y軸的距離是2,則點P的坐標為( )
A. (4,﹣2) B. (﹣4,2) C. (﹣2,4) D. (2,﹣4)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com