
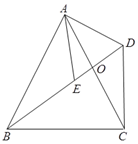
【題目】如圖,四邊形ABCD中,對角線AC、BD交于點O,AB=AC,點E是BD上一點,且AE=AD,∠EAD=∠BAC.
⑴ 求證:∠ABD=∠ACD;
⑵ 若∠ACB=65°,求∠BDC的度數.
【答案】(1)見解析;(2) 50°
【解析】(1)關鍵全等三角形的判定與性質證明即可;(2)利用三角形的外角性質和三角形的內角和解答即可.
詳解:⑴∵ ∠BAC=∠EAD
∴ ∠BAC-∠EAC=∠EAD-∠EAC
即:∠BAE=∠CA,
在△ABE和△ACD中
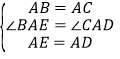
∴ △ABE≌△ACD,
∴ ∠ABD=∠ACD,
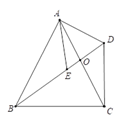
⑵∵ ∠BOC是△ABO和△DCO的外角
∴ ∠BOC=∠ABD+∠BAC,∠BOC=∠ACD+∠BDC
∴ ∠ABD+∠BAC=∠ACD+∠BDC
∵ ∠ABD=∠ACD
∴ ∠BAC=∠BDC,
∵ ∠ACB=65°,AB=AC
∴ ∠ABC=∠ACB=65°,
∴ ∠BAC=180°-∠ABC-∠ACB=180°-65°-65°=50°,
∴ ∠BDC=∠BAC=50°


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
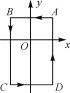
【題目】如圖,在平面直角坐標系中:A(1,1),B(-1,1),C(-1,-2),D(1,-2),現把一條長為2 018個單位長度且沒有彈性的細線(線的粗細忽略不計)的一端固定在點A處,并按A→B→C→D→A→…的規律緊繞在四邊形ABCD的邊上,則細線另一端所在位置的點的坐標是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知直線y= ![]() x+2與x軸交于點A,與y軸交于點C,拋物線y=ax2+4ax+b經過A.C兩點,且與x軸交于另一點B.
x+2與x軸交于點A,與y軸交于點C,拋物線y=ax2+4ax+b經過A.C兩點,且與x軸交于另一點B.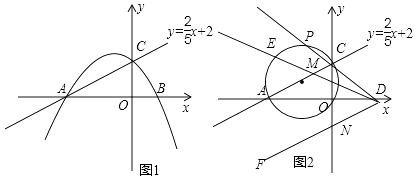
(1)求拋物線的解析式;
(2)若點Q在拋物線上,且△AQC與△BQC面積相等,求點Q的坐標;
(3)如圖2,P為△AOC外接圓上弧ACO的中點,直線PC交x軸于點D,∠EDF=∠ACO,當∠EDF繞點D旋轉時,DE交直線AC于點M,DF交y軸負半軸于點N.請你探究:CN﹣CM的值是否發生變化?若不變,求出其值;若變化,求出變化范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
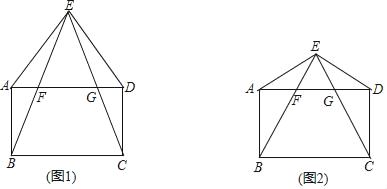
【題目】已知:點E為矩形ABCD外一點,連接AE,DE,且AE=DE,連接EB,EC分別與AD相交于點F,G.
(1)如圖1,求證:∠ABE=∠DCE;
(2)如圖2,若△BCE是等邊三角形,且AE=AB,在不添加任何輔助線的情況下,請直接寫出圖2中四對全等的鈍角三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果一個多位自然數的任意兩個相鄰數位上,右邊數位上的數總比左邊數位上數大1,那么我們把這樣的自然數叫做“相連數”.例如:234,4567,56789,…都是“相連數”.
(1)請直接寫出最大的兩位“相連數”與最小的三位“相連數”,并求它們的差.
(2)若某個“相連數”恰好等于其個位數的469倍,求這個“相連數”.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在某項針對18﹣35歲的青年人每天發微博數量的調查中,設一個人的“日均發微博條數”為m,規定:當0≤m<5時為A級,5≤m<10時為B級,10≤m<15時為C級,m≥15時為D級.現隨機抽取部分符合年齡條件的青年人開展每人“日均發微博條數”的調查,制作圖表如下: 18﹣35歲青年人日均發微博條數統計表
m | 頻數 | 百分數 |
A級(0≤m<5) | 90 | 0.3 |
B級(5≤m<10) | 120 | a |
C級(10≤m<15) | b | 0.2 |
D級(m≥15) | 30 | 0.1 |
請你根據以上信息解答下列問題:
(1)求a,b;
(2)補全頻數分布直方圖.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】實踐探究
在數學實踐課上,小明提出了這樣的問題:分數![]() 可以寫為小數形式,即0.
可以寫為小數形式,即0.![]() 反過來,無限循環小數0.
反過來,無限循環小數0. ![]() 寫成分數形式即為
寫成分數形式即為![]() .那么無限循環小數0.
.那么無限循環小數0. ![]() 應怎樣化為分數呢?
應怎樣化為分數呢?
小明是這樣思考的:
在學習解一元一次方程時,當變形到ax=b(a≠0)形式后,通過系數化1,兩邊同時除以a,得到方程的解x=![]() ,
,![]() 就是分數形式.
就是分數形式.
設0. ![]() =x,即x=0.777…,又10x=7.77…,這里x、0.777…、10x、7.77…存在著關系,根據這一關系我就可以找到相等關系,列出方程.
=x,即x=0.777…,又10x=7.77…,這里x、0.777…、10x、7.77…存在著關系,根據這一關系我就可以找到相等關系,列出方程.
請你閱讀小明的思考過程,把無限循環小數0. ![]() 化為分數的過程寫出來.
化為分數的過程寫出來.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校八年級共有8個班,241名同學,歷史老師為了了解新中考模式下該校八年級學生選修歷史學科的意向,請小紅,小亮,小軍三位同學分別進行抽樣調查.三位同學調查結果反饋如下:
小紅、小亮和小軍三人中,你認為哪位同學的調查結果較好地反映了該校八年級同學選修歷史的意向,請說出理由,并由此估計全年級有意向選修歷史的同學的人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com