
【題目】如圖,∠BAD=∠CAE=90°,AB=AD,AE=AC.
(1)證明:BC=DE;
(2)若AC=12,求四邊形ABCD的面積.

【答案】(1)見解析;(2) 72.
【解析】試題分析:(1)由等角角的余角相等求出∠BAC=∠EAD,根據SAS推出△ABC≌△ADE;(2)由全等三角形的性質得出S△ABC=S△ADE,推出四邊形ABCD的面積=三角形ACE的面積,即可得出答案.
試題解析:(1)∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAC=∠EAD.
在△ABC和△ADE中, 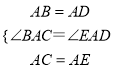 ,
,
∴△ABC≌△ADE(SAS).
∴BC=DE.
(2)∵△ABC≌△ADE ,
∴S△ABC=S△ADE,
∴S四邊形ABCD=S△ABC+S△ACD=S△ADE+S△ACD=S△ACE=![]() ×122=72.
×122=72.


 單元期中期末卷系列答案
單元期中期末卷系列答案科目:初中數學 來源: 題型:
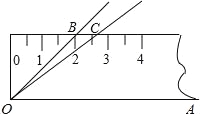
【題目】如圖,將45°的∠AOB按下面的方式放置在一把刻度尺上:頂點O與尺下沿的端點重合,OA與尺下沿重合,OB與尺上沿的交點B在尺上的讀數恰為2cm.若按相同的方式將37°的∠AOC放置在該刻度尺上,則OC與尺上沿的交點C在尺上的讀數約為 cm.(結果精確到0.1cm,參考數據:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點A(﹣5,0),B(3,0).
(1)在y軸上找一點C,使之滿足S△ABC=16,求點C的坐標(要有必要的步驟);
(2)在直角坐標平面上找一點C,能滿足S△ABC=16的C有多少個?這些點有什么特征?
查看答案和解析>>
科目:初中數學 來源: 題型:
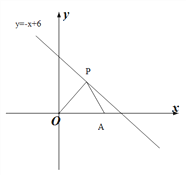
【題目】在平面直角坐標系中,點P(m,n)在第一象限,且在直線y=-x+6上,點A的坐標為(5,0),O是坐標原點,△PAO的面積是S.
(1)求S與m的函數關系式,并畫出函數S的圖象;
(2)小杰認為△PAO的面積可以為15,你認為呢?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com