
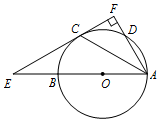
 如圖,AB是⊙O的直徑,C,D是⊙O上兩點,且$\widehat{BC}$=$\widehat{CD}$,過點C的直線CF⊥AD于點F,交AB的延長線于點E,連接AC.
如圖,AB是⊙O的直徑,C,D是⊙O上兩點,且$\widehat{BC}$=$\widehat{CD}$,過點C的直線CF⊥AD于點F,交AB的延長線于點E,連接AC.分析 (1)連接OC,根據等腰三角形的性質得到∠1=∠2,根據圓周角定理得到∠1=∠3,推出OC∥AF,根據切線的判定定理即可得到結論;
(2)由sinE=$\frac{1}{2}$,推出△AEF,△OEC都為含30°的直角三角形;推出△ACF為含30°的直角三角形;由勾股定理可求OF的長.
解答  (1)證明:如圖,連接OC,
(1)證明:如圖,連接OC,
∵OC=OA,
∴∠1=∠2,
∵$\widehat{BC}$=$\widehat{CD}$,
∴∠1=∠3,
∴∠2=∠3,
∴OC∥AF,
∵CF⊥AD,
∴∠CFA=90°,
∴∠OCF=90°,
∴OC⊥EF,
∵OC為⊙O的半徑,
∴EF是⊙O的切線;
(2)解:求解思路如下:
①在Rt△AEF和Rt△OEC中,由sinE=$\frac{1}{2}$,
可得△AEF,△OEC都為含30°的直角三角形;
②由∠1=∠3,可知△ACF為含30°的直角三角形;
③由⊙O的半徑為r,可求OE,AE的長,從而可求CF的長;
④在Rt△COF中,由勾股定理可求OF的長.
點評 本題考查了切線的判定,直角三角形的性質,圓周角定理,平行線的判定和性質,正確的作出輔助線是解題的關鍵.


科目:初中數學 來源: 題型:解答題
 一個不透明的口袋中有三個小球,上面分別標有數字2,3,4,每個小球除數字不同外其他都相同,先從袋中隨機摸出1個小球,記下數字后放回;再從袋中隨機摸出一個小球.用畫樹狀圖(或列表)的方法,求兩次摸出小球上的數字之和為偶數的概率.
一個不透明的口袋中有三個小球,上面分別標有數字2,3,4,每個小球除數字不同外其他都相同,先從袋中隨機摸出1個小球,記下數字后放回;再從袋中隨機摸出一個小球.用畫樹狀圖(或列表)的方法,求兩次摸出小球上的數字之和為偶數的概率.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
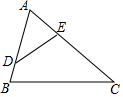 如圖,△ABC中,D、E分別是AB、AC邊上一點,連接DE.請你添加一個條件,使△ADE∽△ABC,則你添加的這一個條件可以是∠ADE=∠B(寫出一個即可).
如圖,△ABC中,D、E分別是AB、AC邊上一點,連接DE.請你添加一個條件,使△ADE∽△ABC,則你添加的這一個條件可以是∠ADE=∠B(寫出一個即可).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 補全解題過程.
補全解題過程.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com