
【題目】如圖,矩形OABC在平面直角坐標系xOy中,點A在x軸的正半軸上,點C在y軸的正半軸上,OA=4,OC=3,若拋物線的頂點在BC邊上,且拋物線經過O,A兩點,直線AC交拋物線于點D.
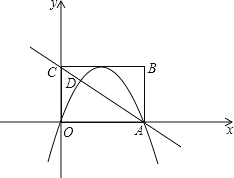
(1)求拋物線的解析式;
(2)求點D的坐標;
(3)若點M在拋物線上,點N在x軸上,是否存在以A,D,M,N為頂點的四邊形是平行四邊形?若存在,求出點N的坐標;若不存在,請說明理由.
【答案】(1)y=-![]() x2+3x;(2) 點D坐標為(1,
x2+3x;(2) 點D坐標為(1,![]() );(3)存在,N1(2,0),N2(6,0),N3(-
);(3)存在,N1(2,0),N2(6,0),N3(-![]() -1,0),N4(
-1,0),N4(![]() -1,0).
-1,0).
【解析】
試題分析:(1)由OA的長度確定出A的坐標,再利用對稱性得到頂點坐標,設出拋物線的頂點形式y=a(x-2)2+3,將A的坐標代入求出a的值,即可確定出拋物線解析式;
(2)設直線AC解析式為y=kx+b,將A與C坐標代入求出k與b的值,確定出直線AC解析式,與拋物線解析式聯立即可求出D的坐標;
(3)存在,分兩種情況考慮:如圖所示,當四邊形ADMN為平行四邊形時,DM∥AN,DM=AN,由對稱性得到M(3,![]() ),即DM=2,故AN=2,根據OA+AN求出ON的長,即可確定出N的坐標;當四邊形ADM′N′為平行四邊形,可得三角形ADQ全等于三角形N′M′P,M′P=DQ=
),即DM=2,故AN=2,根據OA+AN求出ON的長,即可確定出N的坐標;當四邊形ADM′N′為平行四邊形,可得三角形ADQ全等于三角形N′M′P,M′P=DQ=![]() ,N′P=AQ=3,將y=-
,N′P=AQ=3,將y=-![]() 代入得:-
代入得:-![]() =-
=-![]() x2+3x,求出x的值,確定出OP的長,由OP+PN′求出ON′的長即可確定出N′坐標.
x2+3x,求出x的值,確定出OP的長,由OP+PN′求出ON′的長即可確定出N′坐標.
試題解析:(1)設拋物線頂點為E,根據題意OA=4,OC=3,得:E(2,3),
設拋物線解析式為y=a(x-2)2+3,
將A(4,0)坐標代入得:0=4a+3,即a=-![]() ,
,
則拋物線解析式為y=-![]() (x-2)2+3=-
(x-2)2+3=-![]() x2+3x;
x2+3x;
(2)設直線AC解析式為y=kx+b(k≠0),
將A(4,0)與C(0,3)代入得:![]() ,
,
解得: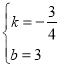 ,
,
故直線AC解析式為y=-![]() x+3,
x+3,
與拋物線解析式聯立得: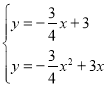 ,
,
解得:![]() 或
或![]() ,
,
則點D坐標為(1,![]() );
);
(3)存在,分兩種情況考慮:
①當點M在x軸上方時,如圖1所示:
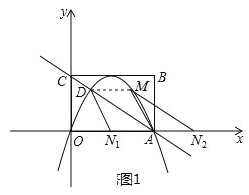
四邊形ADMN為平行四邊形,DM∥AN,DM=AN,
由對稱性得到M(3,![]() ),即DM=2,故AN=2,
),即DM=2,故AN=2,
∴N1(2,0),N2(6,0);
②當點M在x軸下方時,如圖2所示:
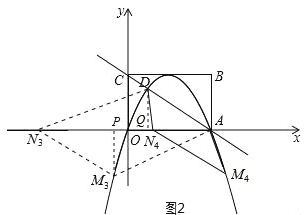
過點D作DQ⊥x軸于點Q,過點M作MP⊥x軸于點P,可得△ADQ≌△NMP,
∴MP=DQ=![]() ,NP=AQ=3,
,NP=AQ=3,
將yM=-![]() 代入拋物線解析式得:-
代入拋物線解析式得:-![]() =-
=-![]() x2+3x,
x2+3x,
解得:xM=2-![]() 或xM=2+
或xM=2+![]() ,
,
∴xN=xM-3=-![]() -1或
-1或![]() -1,
-1,
∴N3(-![]() -1,0),N4(
-1,0),N4(![]() -1,0).
-1,0).
綜上所述,滿足條件的點N有四個:N1(2,0),N2(6,0),N3(-![]() -1,0),N4(
-1,0),N4(![]() -1,0).
-1,0).


 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案 單元加期末復習先鋒大考卷系列答案
單元加期末復習先鋒大考卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,點D、E、F分別是AB、BC、CA的中點,AH是邊BC上的高.
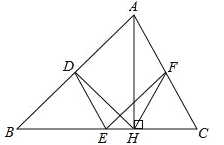
(1)求證:四邊形ADEF是平行四邊形;
(2)求證:∠DHF=∠DEF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(10分)如圖,在直角坐標系中,矩形OABC的頂點O與坐標原點重合,A、C分別在坐標軸上,點B的坐標為(4,2),直線y=﹣![]() x+3交AB,BC分別于點M,N,反比例函數y=
x+3交AB,BC分別于點M,N,反比例函數y=![]() 的圖象經過點M,N.
的圖象經過點M,N.
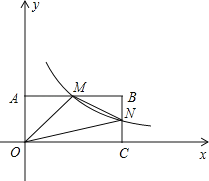
(1)求反比例函數的解析式;
(2)若點P在y軸上,且△OPM的面積與四邊形BMON的面積相等,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場銷售一批襯衫,平均每天可售出20件,每件盈利40元.為了擴大銷售,增加盈利,商場采取了降價措施.假設在一定范圍內,襯衫的單價每降1元,商場平均每天可多售出2件.如果降價后商場銷售這批襯衫每天盈利1250元,那么襯衫的單價降了多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
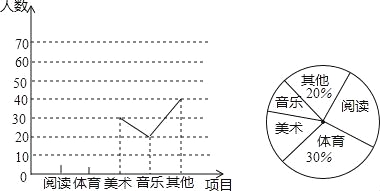
【題目】某學校為了解該校學生的課余活動情況,抽樣調查了部分同學,將所得數據處理后,制成折線統計圖(部分)和扇形統計圖(部分)如下:
(1)在這次研究中,一共調查了 名學生.
(2)補全頻數分布折線圖;
(3)該校共有2200名學生,估計該校學生中愛好閱讀的人數大約是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在□ABCD中,過點D作DE⊥AB于點E,點F在邊CD上,DF=BE,連接AF,BF.
(1)求證:四邊形DEBF是矩形;
(2)若AF平分∠DAB,AE=3,BF=4,求□ABCD的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
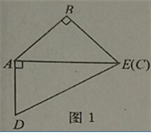
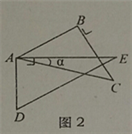
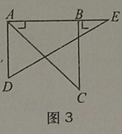
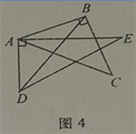
【題目】如圖,取一副三角板按圖1拼接,固定三角板ADE(含30°),將三角板ABC(含45°)繞點A順時針方向旋轉一個大小為α的角(0°<α≤45°),試問:
(1)當∠α=_____度時,能使圖2中的AB∥DE;
(2)當旋轉到AB與AE重疊時(如圖3),則∠α=_____度;
(3)當△ADE的一邊與△ABC的某一邊平行(不共線)時,直接寫出旋轉角α的所有可能的度數;
(4)當0°<α≤45°時,連接BD(如圖4),探求∠DBC+∠CAE+∠BDE的值的大小變化情況,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com