
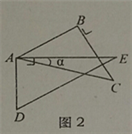
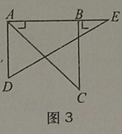
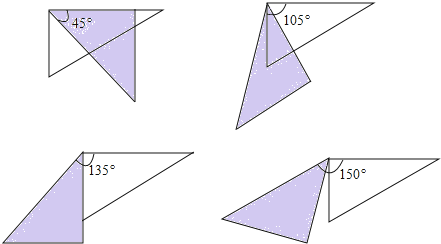
【題目】如圖,取一副三角板按圖1拼接,固定三角板ADE(含30°),將三角板ABC(含45°)繞點A順時針方向旋轉一個大小為α的角(0°<α≤45°),試問:
(1)當∠α=_____度時,能使圖2中的AB∥DE;
(2)當旋轉到AB與AE重疊時(如圖3),則∠α=_____度;
(3)當△ADE的一邊與△ABC的某一邊平行(不共線)時,直接寫出旋轉角α的所有可能的度數;
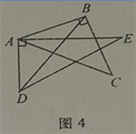
(4)當0°<α≤45°時,連接BD(如圖4),探求∠DBC+∠CAE+∠BDE的值的大小變化情況,并說明理由.
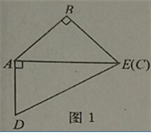
【答案】 15° 45°(3) 15°,45°,105°,135°,150° (4) 保持不變;理由見解析
【解析】試題分析: (1)根據平行線的性質,可得∠BAE=∠E=30°,再根據∠BAC=45°,即可得出∠CAE=45°-30°=15°;
(2)根據當旋轉到AB與AE重疊時,∠α=∠BAC即可得到結果;
(3)要分5種情況進行討論:AD∥BC、DE∥AB、DE∥BC、DE∥AC、AE∥BC,分別畫出圖形,計算出度數即可;
(4)先設BD分別交AC、AE于點M、N,在△AMN中,∠AMN+∠CAE+∠ANM=180,再根據∠ANM=∠E+∠BDE,∠AMN=∠C+∠DBC,得出∠E+∠BDE+∠CAE+∠C+∠DBC=180°,然后根據∠C=30°,∠E=45°,即可得出∠BDE+∠CAE+∠DBC的度數.
試題解析:
(1)如圖2,當AB∥DE時,∠BAE=∠E=30°,
∵∠BAC=45°,
∴∠CAE=45°-30°=15°,
即∠α=15°,
故答案為:15;
(2)當旋轉到AB與AE重疊時,∠α=∠BAC=45°,
故答案為:45;
(3)當△ADE的一邊與△ABC的某一邊平行(不共線)時,旋轉角α的所有可能的度數是:15°,45°,105°,135°,150°;
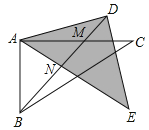
(4)當0°<α<45°,∠BDE+∠CAE+∠DBC=105°,保持不變;理由如下:
設BD分別交AC、AE于點M、N,
在△AMN中,∠AMN+∠CAE+∠ANM=180,
∵∠ANM=∠E+∠BDE,∠AMN=∠C+∠DBC,
∴∠E+∠BDE+∠CAE+∠C+∠DBC=180°,
∵∠C=30°,∠E=45°,
∴∠BDE+∠CAE+∠DBC=105°.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,矩形OABC在平面直角坐標系xOy中,點A在x軸的正半軸上,點C在y軸的正半軸上,OA=4,OC=3,若拋物線的頂點在BC邊上,且拋物線經過O,A兩點,直線AC交拋物線于點D.
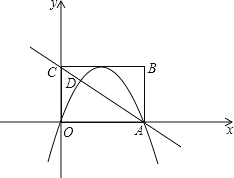
(1)求拋物線的解析式;
(2)求點D的坐標;
(3)若點M在拋物線上,點N在x軸上,是否存在以A,D,M,N為頂點的四邊形是平行四邊形?若存在,求出點N的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示:
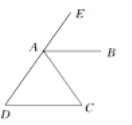
(1)∵________=__________(已知)
∴AB∥CD(同位角相等,兩條直線平行)
(2)∵_________=__________(已知)
∴AB∥CD(內位角相等,兩條直線平行)
(3)∵_________+_________=180(已知)
∴AB∥CD(同旁內角互補,兩條直線平行)
查看答案和解析>>
科目:初中數學 來源: 題型:
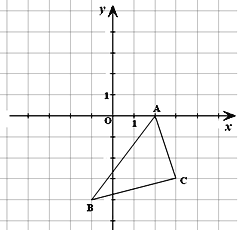
【題目】如圖所示的直角坐標系中,解答下列問題:
(1)分別寫出A、B兩點的坐標;
(2)將△ABC向左平移3個單位長度,再向上平移5個單位長度,畫出平移后的△A1B1C1;
(3)求 △A1B1C1的面積。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,小明所在教學樓的每層高度為3.5米,為了測量旗桿MN的高度,他在教學樓一樓的窗臺A處測得旗桿頂部M的仰角為45°,他在二樓窗臺B處測得M的仰角為31°,已知每層樓的窗臺離該層的地面高度均為1米,求旗桿MN的高度;(結果保留兩位小數)
(參考數據:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學開展“陽光體育一小時”活動,根據學校實際情況,決定開設A:踢毽子;B:籃球;C:跳繩;D:乒乓球四種運動項目.為了解學生最喜歡哪一種運動項目,隨機抽取了一部分學生進行調查,并將調查結果繪制成如下兩個統計圖.請結合圖中的信息解答下列問題:
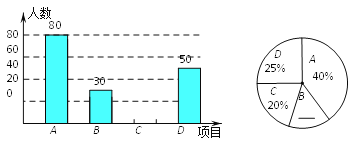
(1)本次共調查了多少名學生?
(2)請將兩個統計圖補充完整.
(3)若該中學有1200名學生,喜歡籃球運動項目的學生約有多少名?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com