
已知某二次函數的圖象與 軸分別相交于點
軸分別相交于點 和點
和點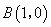 ,
,
與 軸相交于點
軸相交于點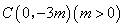 ,頂點為點
,頂點為點 。
。
⑴求該二次函數的解析式(系數用含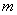 的代數式表示);
的代數式表示);
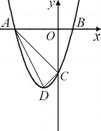
⑵如圖①,當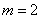 時,點
時,點 為第三象限內拋物線上的一個動點,設
為第三象限內拋物線上的一個動點,設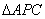 的面積為
的面積為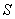 ,試求出
,試求出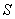 與點
與點 的橫坐標
的橫坐標 之間的函數關系式及
之間的函數關系式及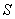 的最大值;
的最大值;
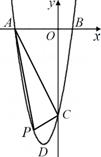
⑶如圖②,當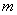 取何值時,以
取何值時,以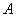 、
、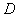 、
、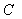 三點為頂點的三角形與
三點為頂點的三角形與 相似?
相似?
 | |||||
| |||||
| |||||
 解:⑴∵該二次函數的圖象與
解:⑴∵該二次函數的圖象與 軸分別相交于點
軸分別相交于點 和點
和點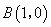 ,
,
∴設該二次函數的解析式為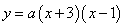
∵該二次函數的圖象與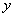 軸相交于點
軸相交于點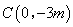 ,
,
∴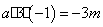 ,故
,故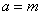
∴該二次函數的解析式為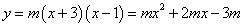
⑵當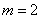 時,點
時,點 的坐標為
的坐標為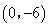 ,該二次函數的解析式為
,該二次函數的解析式為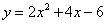
∵點 的坐標為
的坐標為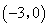 ,點
,點 的坐標為
的坐標為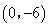
∴直線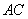 的解析式為
的解析式為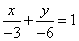 ,即
,即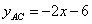
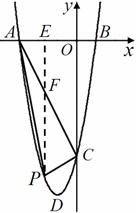
過點 作
作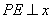 軸于點
軸于點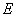 ,交
,交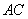 于點
于點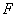
∵點 為第三象限內拋物線上的一個動點且點
為第三象限內拋物線上的一個動點且點 的橫坐標為
的橫坐標為
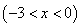
∴點 的坐標為
的坐標為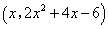 ,點
,點 的坐標為
的坐標為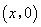 ,點
,點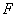 的坐標為
的坐標為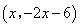
∴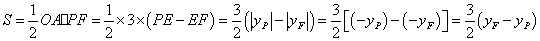
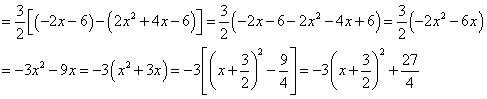
∴當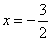 時,
時,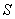 有最大值
有最大值 ;
;
另解: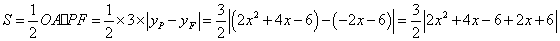
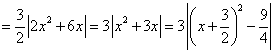
∵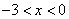 ,∴
,∴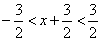 ,∴
,∴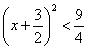 ,∴
,∴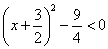 ,
,
∴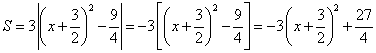 (其余略)
(其余略)
再解: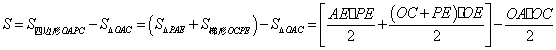
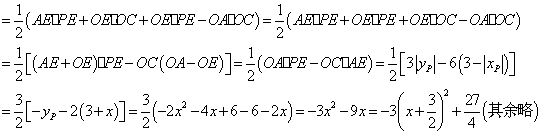
⑶∵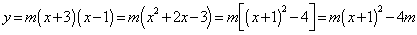 ,∴點
,∴點 的坐標為
的坐標為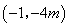
∴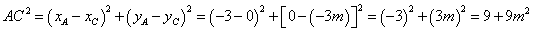
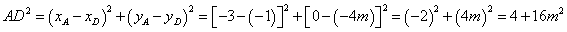
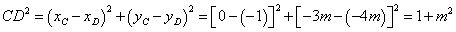
∵ 是直角三角形,∴欲使以
是直角三角形,∴欲使以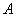 、
、 、
、 三點為頂點的三角形與
三點為頂點的三角形與 相似,必有
相似,必有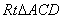
①若在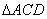 中,
中,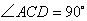 ,則
,則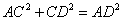 ,即
,即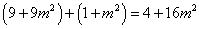
化簡整理得: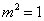 ,∵
,∵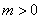 ,∴
,∴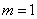 (舍去負值)
(舍去負值)
此時,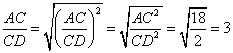 ,
,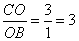 ,∴
,∴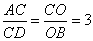
∵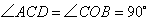 且
且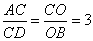 ,∴
,∴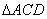 與
與 相似,符合題意;
相似,符合題意;
②若在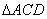 中,
中,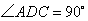 ,則
,則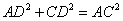 ,即
,即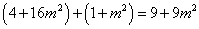
化簡整理得: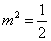 ,∵
,∵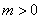 ,∴
,∴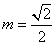 (舍去負值)
(舍去負值)
此時,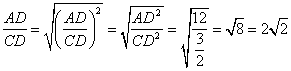 ,
,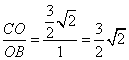 ,∴
,∴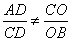
雖然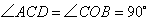 ,但是
,但是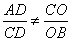 ,∴
,∴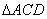 與
與 不相似,應舍去;
不相似,應舍去;
∴綜上所述,只有當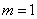 時,以
時,以 、
、 、
、 三點為頂點的三角形與
三點為頂點的三角形與 相似。
相似。


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
如圖1,P(m,n)是拋物線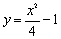 上任意一點, l是過點(0,
上任意一點, l是過點(0,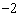 )且與x軸平行的直線,過點P作直線PH⊥l,垂足為H.
)且與x軸平行的直線,過點P作直線PH⊥l,垂足為H.
【探究】
(1)填空:當m=0時,OP= ,PH= ;當m=4時,OP= ,PH= ;
【證明】
(2)對任意m,n,猜想OP 與PH的大小關系,并證明你的猜想.
【應用】
(3)如圖2,已知線段AB=6,端點A,B在拋物線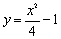 上滑動,求A,B兩點到直線l的距離之和的最小值.
上滑動,求A,B兩點到直線l的距離之和的最小值.
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
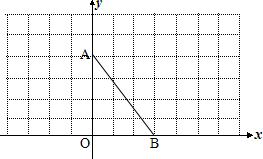
如圖,在直角坐標系中,A(0,4)、C(3,0)
(1) ① 畫出線段AC關于y軸對稱線段AB
② 將線段CA繞點C順時針旋轉一個角,得到對應線段CD,使得AD∥x軸,請畫出線段CD
(2) 若直線y=kx平分(1)中四邊形ABCD的面積,請直接寫出實數k的值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com