
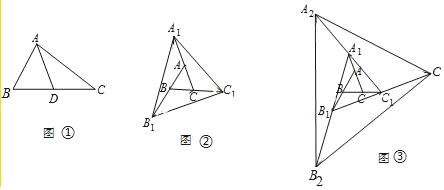
【題目】如圖①,△ABC中,AD為BC邊上的中線,則有S△ABD=S△ACD,許多面積問題可以轉化為這個基本模型解答.如圖②,已知△ABC的面積為1,把△ABC各邊均順次延長一倍,連結所得端點,得到△A1B1C1,即將△ABC向外擴展了一次,則擴展一次后的△A1B1C1的面積是_____,如圖③,將△ABC向外擴展了兩次得到△A2B2C2,……,若將△ABC向外擴展了n次得到△AnBnn,則擴展n次后得到的△AnBnn面積是_____.
 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:初中數學 來源: 題型:
【題目】在一個不透明的盒子里裝有只有顏色不同的黑、白兩種球共40個,小穎做摸球實驗,她將盒子里面的球攪勻后從中隨機摸出一個球記下顏色,再把它放回盒子中,不斷重復上述過程,下表是“摸到白球”的頻率折線統計圖:

(1)請估計:當![]() 很大時,摸到白球的頻率將會接近 (精確到0.01);假如你摸一次,你摸到白球的概率
很大時,摸到白球的頻率將會接近 (精確到0.01);假如你摸一次,你摸到白球的概率![]() .
.
(2)試估算盒子里白、黑兩種顏色的球各有多少只?
(3)在(2)條件下如果要使摸到白球的概率為![]() ,需要往盒子里再放入多少個白球?
,需要往盒子里再放入多少個白球?
查看答案和解析>>
科目:初中數學 來源: 題型:
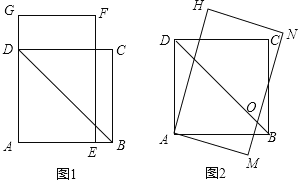
【題目】如圖1,四邊形ABCD是邊長為![]() 的正方形,矩形AEFG中AE=4,∠AFE=30°。將矩形AEFG繞點A順時針旋轉15°得到矩形AMNH(如圖2),此時BD與MN相交于點O.
的正方形,矩形AEFG中AE=4,∠AFE=30°。將矩形AEFG繞點A順時針旋轉15°得到矩形AMNH(如圖2),此時BD與MN相交于點O.
(1)求∠DOM的度數;
(2)圖2中,求D、N兩點間的距離;
(3)若將矩形AMNH繞點A再順時針旋轉15°得到矩形APQR,此時點B在矩形APQR的內部、外部還是邊上?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知銳角△ABC內接于⊙O,連接AO并延長交BC于點D.
(1)求證:∠ACB+∠BAD=90°;
(2)過點D作DE⊥AB于E,若∠ADC=2∠ACB.求證:AC=2DE.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場購進一批單價為4元/件的日用品。若按每件5元的價格出售,每月能賣出3萬件;若按每件6元的價格銷售,每月能賣出2萬件;假定每月的銷售件數y(萬件)與價格x(元/件)之間滿足一次函數關系.
(1)試求y與x的函數關系式;
(2)當銷售價格定為多少時,才能使每月的利潤最大?每月的最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
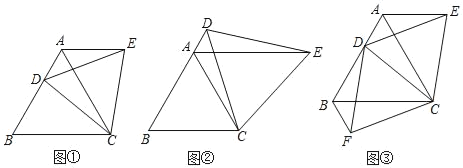
【題目】(1)操作發現:如圖①,點D是等邊△ABC的邊AB上一動點(點D與點B不重合),連接CD,以CD為邊在CD上方作等邊△CDE,連接AE,則AE與BD有怎樣的數量關系?說明理由.
(2)類比猜想:如圖②,若點D是等邊△ABC的邊BA延長線上一動點,連接CD,以CD為邊在CD上方作等邊△CDE,連接AE,請直接寫出AE與BD滿足的數量關系,不必說明理由;
(3)深入探究:如圖③,點D是等邊△ABC的邊AB上一動點(點D與點B不重合),連接CD,以CD為邊分別在CD上方、下方作等邊△CDE和等邊△CDF,連接AE,BF則AE,BF與AB有怎樣的數量關系?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人玩贏卡片游戲,工具是一個如圖所示的轉盤(等分成8份),游戲規定:自由轉動的轉盤,當轉盤停止后指針指向字母“A”,則甲輸給乙2張卡片,若指針指向字母“B”,則乙輸給甲3張卡片;若指針指向字母“C”,則乙輸給甲1張卡片(如果指針恰好指在分割線上,那么重轉一次,直到指針指向某一區域為止).
(1)轉動一次轉盤,求甲贏取1張卡片的概率;
(2)轉動一次轉盤,求乙贏取2張卡片的概率;
(3)轉動一次轉盤,求甲贏取卡片的概率.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com