
【題目】某商場購進一批單價為4元/件的日用品。若按每件5元的價格出售,每月能賣出3萬件;若按每件6元的價格銷售,每月能賣出2萬件;假定每月的銷售件數y(萬件)與價格x(元/件)之間滿足一次函數關系.
(1)試求y與x的函數關系式;
(2)當銷售價格定為多少時,才能使每月的利潤最大?每月的最大利潤是多少?
【答案】(1)y與x的函數關系式為y=-x+8;
(2)當銷售價格定為6元時,才能使每月的利潤最大,每月的最大利潤是4萬元.
【解析】試題分析:(1)設y=kx+b,再由題目已知條件不難得出解析式;(2)設利潤為W,將W用含x的式子表示出來,W為關于x的二次函數,要求最值,將解析式化為頂點式即可求出.
試題解析:
解:(1)設y=kx+b,
根據題意得: ![]() ,
,
解得:k=-1,b=8,
所以,y與x的函數關系式為y=-x+8;
(2)設利潤為W,則W=(x-4)(-x+8)=-(x-6)2+4,
因為a=-1<0,所以當x=6時,W最大為4萬元.
當銷售價格定為6元時,才能使每月的利潤最大,每月的最大利潤是4萬元.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
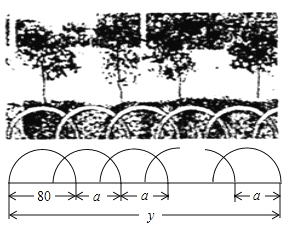
【題目】如圖所示,某花園護欄是用直徑為![]() 的半圓形條鋼組制而成,且每增加一個半圓形條鋼,護欄長度增加
的半圓形條鋼組制而成,且每增加一個半圓形條鋼,護欄長度增加![]() ,設半圓形條鋼的個數為
,設半圓形條鋼的個數為![]() (
(![]() 為正整數),護欄總長度為
為正整數),護欄總長度為![]() .
.
(1)若![]() .
.
①當![]() 時,y=______
時,y=______![]() ;
;
②寫出![]() 與
與![]() 之間的函數關系式為_______.
之間的函數關系式為_______.
(2)若護欄總長度為![]() ,則當
,則當![]() 時,所用半圓形條鋼個數為_______;
時,所用半圓形條鋼個數為_______;
(3)若護欄總長度不變,則當![]() 時,用了
時,用了![]() 個半圓形條鋼;當
個半圓形條鋼;當![]() 時,用了
時,用了![]() 個半圓形條鋼.請求出
個半圓形條鋼.請求出![]() 與
與![]() 之間的關系式.
之間的關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ACB和△ECD都是等腰直角三角形,CA=CB,CD=CE,△ACB的頂點A在△ECD的斜邊DE上,連接BD.

(1)求證:BD=AE;
(2)若AE=5cm,AD=7cm,求AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,D是AB的中點,E在邊AC上,若D與C關于BE成軸對稱,則下列結論:①∠A=30°;②△ABE是等腰三角形;③點B到∠CED的兩邊距離相等.其中正確的有( )
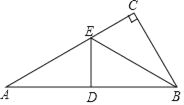
A. 0個B. 1個C. 2個D. 3個
查看答案和解析>>
科目:初中數學 來源: 題型:
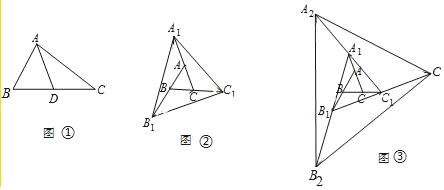
【題目】如圖①,△ABC中,AD為BC邊上的中線,則有S△ABD=S△ACD,許多面積問題可以轉化為這個基本模型解答.如圖②,已知△ABC的面積為1,把△ABC各邊均順次延長一倍,連結所得端點,得到△A1B1C1,即將△ABC向外擴展了一次,則擴展一次后的△A1B1C1的面積是_____,如圖③,將△ABC向外擴展了兩次得到△A2B2C2,……,若將△ABC向外擴展了n次得到△AnBnn,則擴展n次后得到的△AnBnn面積是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=13 cm,AC=20 cm,BC邊上的高為12 cm,則△ABC的面積是
A.126 cm2 或66 cm2B.66 cm2C.120 cm2D.126cm2
查看答案和解析>>
科目:初中數學 來源: 題型:
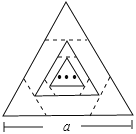
【題目】邊長為a的等邊三角形,記為第1個等邊三角形,取其各邊的三等分點,順次連接得到一個正六邊形,記為第1個正六邊形,取這個正六邊形不相鄰的三邊中點,順次連接又得到一個等邊三角形,記為第2個等邊三角形,取其各邊的三等分點,順次連接又得到一個正六邊形,記為第2個正六邊形(如圖),…,按此方式依次操作,則第6個正六邊形的邊長為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com