Question

（本題10分）如圖，拋物線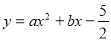經過A（﹣1，0），B（5，0）兩點．

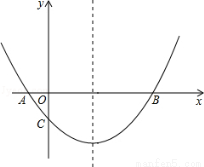
（1）求拋物線的解析式；

（2）在拋物線的對稱軸上有一點P，使PA+PC的值最小，求點P的坐標；

（3）點M為x軸上一動點，在拋物線上是否存在一點N，使以A，C，M，N四點構成的四邊形為平行四邊形？若存在，求點N的坐標；若不存在，請說明理由．

Answer 1

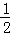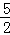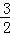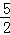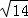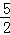（1）拋物線的解析式為：y=x2﹣2x﹣；（2）P（2，﹣）；（3）符合條件的點N的坐標為（4，﹣），（2+，）或（2﹣，）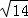

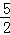【解析】

試題分析：（1）把A（﹣1，0），B（5，0）代入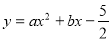，得

解得：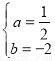

∴拋物線的解析式為：y=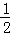x2﹣2x﹣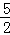； 3分

（2）∵拋物線的解析式為：y=x2﹣2x﹣，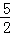

∴其對稱軸為直線x=﹣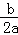=﹣=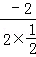2，

連接BC，如圖1所示，

∵B（5，0），C（0，﹣），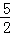

∴設直線BC的解析式為y=kx+b（k≠0），

∴，

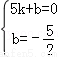解得，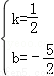

∴直線BC的解析式為y=x﹣，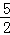

當x=2時，y=1﹣=﹣，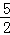

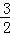∴P（2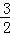，﹣）； 3分

（3）存在．

如圖2所示，

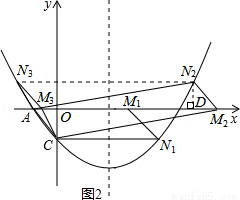
①當點N在x軸下方時，

∵拋物線的對稱軸為直線x=2，C（0，﹣），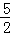

∴N1（4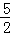，﹣）； 2分

②當點N在x軸上方時，

如圖，過點N作ND⊥x軸于點D，

在△AND與△MCO中，

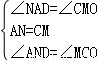
∴△AND≌△MCO（ASA），

∴ND=OC=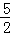，即N點的縱坐標為．

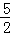∴x2﹣2x﹣=，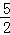

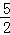解得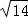x=2+或x=2﹣，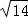

∴N2（2+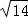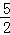，），N3（2﹣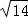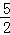，）． 2分

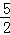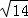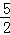綜上所述，符合條件的點N的坐標為（4，﹣），（2+，）或（2﹣，）．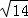

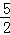考點:二次函數的綜合運用