
【題目】如圖,⊙O為△ABC的外接圓,直線l與⊙O相切與點P,且l∥BC.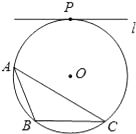
(1)請僅用無刻度的直尺,在⊙O中畫出一條弦,使這條弦將△ABC分成面積相等的兩部分(保留作圖痕跡,不寫作法);
(2)請寫出證明△ABC被所作弦分成的兩部分面積相等的思路.
【答案】
(1)解:如圖所示:
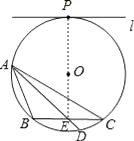
(2)解:∵直線l與⊙O相切與點P,∴OP⊥l,∵l∥BC,∴PE⊥BC,
∴BE=CE,∴弦AE將△ABC分成面積相等的兩部分.
【解析】(1)根據垂徑定理作PE⊥BC于E即可得答案;
(2)利用根據垂徑定理可知BE=CE,即E為BC中點,再由三角形的中線把三角形分成面積相等的兩部分可得出結論.
【考點精析】根據題目的已知條件,利用三角形的“三線”和垂徑定理的相關知識可以得到問題的答案,需要掌握1、三角形角平分線的三條角平分線交于一點(交點在三角形內部,是三角形內切圓的圓心,稱為內心);2、三角形中線的三條中線線交于一點(交點在三角形內部,是三角形的幾何中心,稱為中心);3、三角形的高線是頂點到對邊的距離;注意:三角形的中線和角平分線都在三角形內;垂徑定理:平分弦(不是直徑)的直徑垂直于弦,并且平分弦所對的兩條弧.


科目:初中數學 來源: 題型:
【題目】如圖,點A、B都在數軸上,O為原點.
(1)點B表示的數是_________________;
(2)若點B以每秒2個單位長度的速度沿數軸向右運動,則2秒后點B表示的數是________;
(3)若點A、B分別以每秒1個單位長度、3個單位長度的速度沿數軸向右運動,而點O不動,t秒后,A、B、O三個點中有一個點是另外兩個點為端點的線段的中點,求t的值.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 在 數軸上對應的數分別用
在 數軸上對應的數分別用![]() 表示,且
表示,且![]() .
.![]() 是數軸的一動點.
是數軸的一動點.
⑴在數軸上標出![]() 的位置,并求出
的位置,并求出![]() 之間的距離;
之間的距離;
⑵數軸上一點![]() 距
距![]() 點24個單位的長度,其對應的數
點24個單位的長度,其對應的數![]() 滿足
滿足![]() ,當
,當![]() 點滿足
點滿足![]() 時,求
時,求![]() 點對應的數.
點對應的數.
⑶動點![]() 從原點開始第一次向左移動1個單位,第二次向右移動3個單位長度,第三次向左移動5個單位長度,第四次向右移動7個單位長度,……點
從原點開始第一次向左移動1個單位,第二次向右移動3個單位長度,第三次向左移動5個單位長度,第四次向右移動7個單位長度,……點![]() 能移動到與
能移動到與![]() 或
或![]() 重合的位置嗎?若能,請探究第幾次移動時重合;若不能,請說明理由.
重合的位置嗎?若能,請探究第幾次移動時重合;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算下列各題:
(1)(﹣1)2018﹣2(π﹣1)0+(﹣![]() )﹣2
)﹣2
(2)(2a﹣4)(![]() a+5)﹣2(a﹣10)
a+5)﹣2(a﹣10)
(3)(2x+3y)(﹣2x+3y)﹣(x﹣3y)2
(4)(4x3y﹣6x2y2+12xy3)÷2xy
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】大家已經知道,完全平方公式和平方差公式可以用平面幾何圖形的面積來表示,實際上還有一些代數恒等式也可以用這種形式表示,例如:2x(x+y)=2x2+2xy就可以用圖的面積表示.
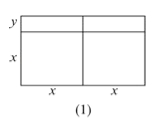
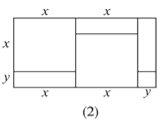
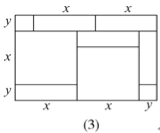
(1)請寫出圖(2)所表示的代數恒等式: _______ ;
(2)請寫出圖(3)所表示的代數恒等式: ________ ;
(3)試畫出一個幾何圖形,使它的面積能表示(x+y)(x+3y)=x2+4xy+3y2.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:拋物線y=x2+(2m-1)x+m2-1經過坐標原點,且當x<0時,y隨x的增大而減小.
(1)求拋物線的解析式;
(2)結合圖象寫出y<0時,對應的x的取值范圍;
(3)設點A是該拋物線上位于x軸下方的一個動點,過點A作x軸的平行線交拋物線于另一點D,再作AB⊥x軸于點B,DC⊥x軸于點C.當BC=1時,直接寫出矩形ABCD的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】南宋數學家楊輝在研究(a+b)n展開式各項的系數時,采用了特殊到一般的方法,他將(a+b)0,(a+b)1,(a+b)2,(a+b)3,…,展開后各項的系數畫成如圖所示的三角陣,在數學上稱之為楊輝三角.已知(a+b)0=1,(a+b)1=a+b,(a+b)2=a2+2ab+b2,(a+b)3=a3+3a2b+3ab2+b3.按楊輝三角寫出(a+b)5的展開式是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的袋子中裝有紅、白兩種顏色的小球,這些球除顏色外都相同,其中紅球有2個,若從中隨機摸出一個球,這個球是白球的概率為 ![]() .
.
(1)求袋子中白球的個數;(請通過列式或列方程解答)
(2)隨機摸出一個球后,放回并攪勻,再隨機摸出一個球,求兩次都摸到相同顏色的小球的概率.(請結合樹狀圖或列表解答)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com