
 如圖,△ABC的面積為1.第一次操作:分別延長AB,BC,CA至點A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,順次連接A1,B1,C1,得到△A1B1C1.第二次操作:分別延長A1B1,B1C1,C1A1至點A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,順次連接A2,B2,C2,得到△A2B2C2,…按此規律,要使得到的三角形的面積超過2017,最少經過多少次操作( )
如圖,△ABC的面積為1.第一次操作:分別延長AB,BC,CA至點A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,順次連接A1,B1,C1,得到△A1B1C1.第二次操作:分別延長A1B1,B1C1,C1A1至點A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,順次連接A2,B2,C2,得到△A2B2C2,…按此規律,要使得到的三角形的面積超過2017,最少經過多少次操作( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 先根據已知條件求出△A1B1C1及△A2B2C2的面積,再根據兩三角形的倍數關系求解即可.
解答 解:△ABC與△A1BB1底相等(AB=A1B),高為1:2(BB1=2BC),故面積比為1:2,
∵△ABC面積為1,
∴S△A1B1B=2.
同理可得,S△C1B1C=2,S△AA1C=2,
∴S△A1B1C1=S△C1B1C+S△AA1C+S△A1B1B+S△ABC=2+2+2+1=7;
同理可證△A2B2C2的面積=7×△A1B1C1的面積=49,
第三次操作后的面積為7×49=343,
第四次操作后的面積為7×343=2401.
故按此規律,要使得到的三角形的面積超過2017,最少經過4次操作.
故選A.
點評 此題考查了三角形的面積,此題屬規律性題目,解答此題的關鍵是找出相鄰兩次操作之間三角形面積的關系,再根據此規律求解即可.


科目:初中數學 來源: 題型:解答題
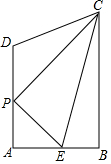 如圖,在梯形ABCD中,AD∥BC,∠A=90°,AB=6,BC=10,AD=7,點P在邊AD上運動(不與點A,D重合),E是邊AB上一點,連結PC,PE,EC.
如圖,在梯形ABCD中,AD∥BC,∠A=90°,AB=6,BC=10,AD=7,點P在邊AD上運動(不與點A,D重合),E是邊AB上一點,連結PC,PE,EC.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在坐標系中放置一菱形OABC,已知∠ABC=60°,點B在y軸上,OA=1,先將菱形OABC沿x軸的正方向無滑動翻轉,每次翻轉60°,連續翻轉2017次,點B的落點依次為B1,B2,B3,…,則B2017的坐標為( )
如圖,在坐標系中放置一菱形OABC,已知∠ABC=60°,點B在y軸上,OA=1,先將菱形OABC沿x軸的正方向無滑動翻轉,每次翻轉60°,連續翻轉2017次,點B的落點依次為B1,B2,B3,…,則B2017的坐標為( )| A. | (1345,0) | B. | (1345.5,$\frac{\sqrt{3}}{2}$) | C. | (1345,$\frac{\sqrt{3}}{2}$) | D. | (1345.5,0) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com