【題目】如圖，在△ABC中，AD為∠BAC的平分線，DE⊥AB于E，DF⊥AC于F，
（1）證明AE=AF；
（2）若△ABC面積是36cm2，AB=10cm，AC=8cm，求DE的長．
【答案】(1)見解析；（2）4
【解析】
本題主要考察角平分線的性質定理和三角形面積的求法，可以根據角平分線的性質定理結合全等進行證明.
（1）證明：∵在△ABC中，AD為∠BAC的平分線，DE⊥AB，DF⊥AC，
∴∠EAD=∠FAD，∠AED=∠AFD=90°，AD=AD
∴△ADE
△ADF，
∴AE=AF；
（2）解：∵在△ABC中，AD為∠BAC的平分線，DE⊥AB，DF⊥AC，
∴DE=DF，
∵△ABC面積是36cm2，AB=10cm，AC=8cm，
∴S△ABC=S△ADB+S△ACD=
ABDE+ACDF=DE（AB+AC）=×DE×（10+8）=9DE=36，
∴DE=4（cm）．
科目：初中數學 來源： 題型：
【題目】已知邊長為m的正方形面積為12，則下列關于m的說法中：①m2是有理數；②m的值滿足m2﹣12＝0；③m滿足不等式組
；④m是12的算術平方根. 正確有幾個（ ）
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某景區的三個景點A、B、C在同一線路上．甲、乙兩名游客從景點A出發，甲步行到景點C;乙乘景區觀光車先到景點B，在B處停留一段時間后，再步行到景點C，甲、乙兩人同時到達景點C．甲、乙兩人距景點A的路程y(米)與甲出發的時間x(分)之間的函數圖象如圖所示．
（1）乙步行的速度為_ __米/分．
（2）求乙乘景區觀光車時y與x之間的函數關系式．
（3）甲出發多長時間與乙第一次相遇?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在四邊形ABCD中，AD∥BC，∠A=90°，CE⊥BD于E，AB=EC．
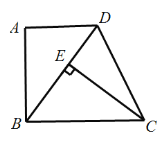
（1）求證：△ABD≌△ECB；
（2）若∠EDC=65°，求∠ECB的度數；
（3）若AD=3，AB=4，求DC的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，在△ABC中，AB=AC，AB的垂直平分線DE分別交AB、AC于D、E．
（1）若AC=12，BC=10，求△EBC的周長；
（2）若∠A=40°，求∠EBC的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下列材料：
情形展示：
情形一：如圖
，在
中，沿等腰三角形ABC的頂角
的平分線
折疊，若點B與點C重合，則稱是的“好角”，如圖
，在中，先沿的平分線折疊，剪掉重復部分，再將余下部分沿
的平分線
折疊，若點
與點C重合，則稱是的“好角”．
情形二：如圖
，在中，先沿的平分線折疊，剪掉重復部分，再將余下部分沿的平分線
折疊，剪掉重復部分
重復折疊n次，最終若點
與點C重合，則稱是的“好角”，探究發現：
不妨設
如圖，若是的“好角”，則
與
的數量關系是：______．
如圖，若是的“好角”，則與的數量關系是：______．
如圖，若是的“好角”，則與的數量關系是：______．
應用提升：
如果一個三角形的三個角分別為
，
，
，我們發現和的兩個角都是此三角形的“好角”；如果有一個三角形，它的三個角均是此三角形的“好角”，且已知最小的角是
，求另外兩個角的度數．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
