【題目】如圖，在四邊形ABCD中，AD∥BC，∠A=90°，CE⊥BD于E，AB=EC．
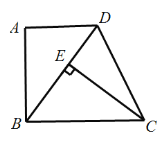
（1）求證：△ABD≌△ECB；
（2）若∠EDC=65°，求∠ECB的度數；
（3）若AD=3，AB=4，求DC的長．
【答案】（1）證明見解析；（2）40°；（3）2
．
【解析】
試題分析：（1）由AD∥BC，得到∠ADB=∠EBC，又因為∠A=∠CEB=90°，推出△ABD≌△ECB；
（2）根據等腰三角形的性質和直角三角形的性質得到結果；
（3）由全等三角形的性質得到對應邊相等，利用勾股定理解出結果．
試題解析：（1）∵AD∥BC，
∴∠ADB=∠EBC，
∵∠A=∠CEB=90°，
在△ABD與△CEB中，
，
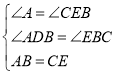∴△ABD≌△ECB；
（2）由（1）證得△ABD≌△ECB，
∴BD=BC，
∴∠BCD=∠BDC=65°，
∵∠DCE=90°-65°=25°，
∴∠ECB=40°；
（3）由（1）證得△ABD≌△ECB，
∴CE=AB=4，BE=AB=3，
∴BD=BC=
=5，
∴DE=2，
∴CD=
=2．
科目：初中數學 來源： 題型：
【題目】小林在某商店購買商品A、B共三次，只有一次購買時，商品A、B同時打折（折扣相同），其余兩次均按標價購買．三次購買商品A、B的數量和費用如下表：
購買商品A的數量/個 | 購買商品B的數量/個 | 購買總費用/元 | |
第一次購物 | 6 | 5 | 1140 |
第二次購物 | 3 | 7 | 1110 |
第三次購物 | 9 | 8 | 1062 |
(1)小林以折扣價購買商品A、B是第 次購物；
(2)求出商品A、B的標價；
(3)若商品A、B的折扣相同，問商店是打幾折出售這兩種商品的?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，Rt△ABC中，∠C=90°，AC=
，tanB=
．半徑為2的⊙C， 分別交AC、BC于點D、E，得到
.
（1）求證：AB為⊙C的切線；
（2）求圖中陰影部分的面積.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】課外閱讀是提高學生素養的重要途徑,某校為了了解學生課外閱讀情況,隨機抽查了50名學生,統計他們平均每天課外閱讀時間(t小時),根據t的長短分為A,B,C,D四類.下面是根據所抽查的人數繪制的兩幅不完整的統計圖表,請根據圖中提供的信息,解答下面的問題：
(1)求表格中的a值,并在圖中補全條形統計圖；
(2)該校現有1300名學生,請你估計該校共有多少學生課外閱讀時間不少于1小時.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，O為直線AB上一點，OC平分∠AOE，∠DOE=90°，則以下結論正確的有____________．（只填序號）
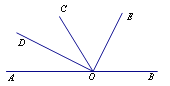
①∠AOD與∠BOE互為余角；
②OD平分∠COA；
③∠BOE=56°40′，則∠COE=61°40′；
④∠BOE=2∠COD．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某縣教育局今年體育測試中，從某校畢業班中抽取男，女學生各15人進行三項體育成績復查測試．在這個問題中，下列敘述正確的是（ ）
A.該校所有畢業班學生是總體B.所抽取的30名學生是樣本
C.樣本的容量是15D.個體指的是畢業班每一個學生的體育測試成績
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一次函數y1=k1x+b（k1≠0）的圖象分別與x軸，y軸相交于點A，B，與反比例函數y2=
的圖象相交于點C（﹣4，﹣2），D（2，4）．
（1）求一次函數和反比例函數的表達式；
（2）當x為何值時，y1＞0；
（3）當x為何值時，y1＜y2，請直接寫出x的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】完成下面的證明：
已知：如圖，AB∥DE，求證：∠D+∠BCD﹣∠B=180°，
證明：過點C作CF∥AB．
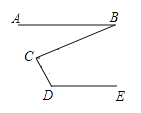
∵AB∥CF（已知），
∴∠B= （ ）．
∵AB∥DE，CF∥AB（ 已知 ），
∴CF∥DE （ ）
∴∠2+ =180° （ ）
∵∠2=∠BCD﹣∠1，
∴∠D+∠BCD﹣∠B=180° （ ）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了豐富學生課余生活，某區教育部門準備在七年級開設興趣課堂．為了了解學生對音樂、書法、球類、繪畫這四個興趣小組的喜愛情況，在全區進行隨機抽樣調查，并根據收集的數據繪制了下面兩幅統計圖(信息不完整)，請根據圖中提供的信息，解答下面的問題：
(1)此次共調查了多少名同學？
(2)將條形圖補充完整，并計算扇形統計圖中音樂部分的圓心角的度數
(3)如果該區七年級共有2000名學生參加這4個課外興趣小組，而每名教師最多只能輔導本組的20名學生，則繪畫興趣小組至少需要準備多少名教師？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com