
 如圖,廣安市防洪指揮部發現渠江邊一處長400米,高8米,背水坡的坡角為45°的防洪大堤(橫截面為梯形ABCD)急需加固.經調查論證,防洪指揮部專家組制定的加固方案是:背水坡面用土石進行加固,并使上底加寬2米,加固后,背水坡EF的坡比i=1:2.
如圖,廣安市防洪指揮部發現渠江邊一處長400米,高8米,背水坡的坡角為45°的防洪大堤(橫截面為梯形ABCD)急需加固.經調查論證,防洪指揮部專家組制定的加固方案是:背水坡面用土石進行加固,并使上底加寬2米,加固后,背水坡EF的坡比i=1:2.
 ,
, ×(2+10)×8×400=19200(立方米).
×(2+10)×8×400=19200(立方米).

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
 時,求x值.
時,求x值.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖是一個由多個相同的小正方形堆積而成的幾何體,從上面看得到平面圖形,小正方形中的數字表示在該位置的小正方體的個數,請你畫出該幾何體從正面看到和從左面看到所得的平面圖形.
如圖是一個由多個相同的小正方形堆積而成的幾何體,從上面看得到平面圖形,小正方形中的數字表示在該位置的小正方體的個數,請你畫出該幾何體從正面看到和從左面看到所得的平面圖形.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,張大爺要圍成一個矩形ABCD花圃.花圃的一邊AD利用足夠長的墻,另三邊恰好用總長為36米的籬笆圍成.設AB的長為x米,矩形ABCD的面積為S平方米.
如圖,張大爺要圍成一個矩形ABCD花圃.花圃的一邊AD利用足夠長的墻,另三邊恰好用總長為36米的籬笆圍成.設AB的長為x米,矩形ABCD的面積為S平方米.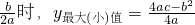 ].
].查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com