
【題目】如圖,將等邊![]() 沿
沿![]() 翻折得
翻折得![]() ,
,![]() ,點
,點![]() 為直線
為直線![]() 上的一個動點,連接
上的一個動點,連接![]() ,將線段
,將線段![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 的角度后得到對應的線段
的角度后得到對應的線段![]() (即
(即![]() ),
),![]() 交
交![]() 于點
于點![]() ,則下列結論:①
,則下列結論:①![]() ;②
;②![]() ;③當
;③當![]() 為線段
為線段![]() 的中點時,則
的中點時,則![]() ;④四邊形
;④四邊形![]() 的面積為
的面積為![]() ;⑤連接
;⑤連接![]() 、
、![]() ,當
,當![]() 的長度最小時,則
的長度最小時,則![]() 的面積為
的面積為![]() .則說法正確的有________(只填寫序號)
.則說法正確的有________(只填寫序號)

【答案】①②
【解析】
由等邊三角形的性質和折疊的性質,得到四邊形ABCD是菱形,則可以判斷①、②;當點E時AD中點時,可得△CPF是直角三角形,CE=CF=3,得到![]() ,可以判斷③;求出對角線的長度,然后求出菱形的面積,可以判斷④;當點E與點A重合時,DF的長度最小,此時四邊形ACFD是菱形,求出對角線EF和CD的長度,求出面積,可以判斷⑤;即可得到答案.
,可以判斷③;求出對角線的長度,然后求出菱形的面積,可以判斷④;當點E與點A重合時,DF的長度最小,此時四邊形ACFD是菱形,求出對角線EF和CD的長度,求出面積,可以判斷⑤;即可得到答案.
解:根據題意,將等邊![]() 沿
沿![]() 翻折得
翻折得![]() ,如圖:
,如圖:
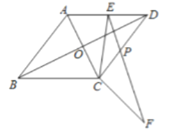
∴![]() ,∠BCD=120°,
,∠BCD=120°,
∴四邊形ABCD是菱形,
∴AC⊥BD,AO=CO,BO=DO;故①、②正確;
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴菱形ABCD的面積=![]() ,故④錯誤;
,故④錯誤;
當點E時AD中點時,CE⊥AD,
∴DE=![]() ,∠DCE=30°,
,∠DCE=30°,
∴![]() ,
,
∵![]() ,
,
∠PCF=120°![]() ,∠F=30°,
,∠F=30°,
∴![]() ,故③錯誤;
,故③錯誤;
當點E與點A重合時,DF的長度最小,如圖:
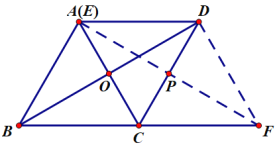
∵AD∥CF,AD=AC=CF,
∴四邊形ACFD是菱形,
∴CD⊥EF,CD=![]() ,
,![]() ,
,
∴![]() ;故⑤錯誤;
;故⑤錯誤;
∴說法正確的有:①②;
故答案為:①②.


 寒假創新型自主學習第三學期寒假銜接系列答案
寒假創新型自主學習第三學期寒假銜接系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,D是BC邊的中點,分別過B、C做射線AD的垂線,垂足分別為E、F,連接BF、CE.
(1)求證:四邊形BECF是平行四邊形;
(2)我們知道S△ABD=S△ACD,若AF=FD,在不添加輔助線的條件下,直接寫出與△ABD、△ACD面積相等的所有三角形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,矩形的一條邊長為x,周長的一半為y,定義(x,y)為這個矩形的坐標。如圖2,在平面直角坐標系中,直線x=1,y=3將第一象限劃分成4個區域,已知矩形1的坐標的對應點A落在如圖所示的雙曲線上,矩形2的坐標的對應點落在區域④中,則下面敘述中正確的是( )

A. 點A的橫坐標有可能大于3
B. 矩形1是正方形時,點A位于區域②
C. 當點A沿雙曲線向上移動時,矩形1的面積減小
D. 當點A位于區域①時,矩形1可能和矩形2全等
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,四邊形ABOC是正方形,點A的坐標為(1,1),![]() 是以點B為圓心,BA為半徑的圓弧;
是以點B為圓心,BA為半徑的圓弧;![]() 是以點O為圓心,OA1為半徑的圓弧;
是以點O為圓心,OA1為半徑的圓弧;![]() 是以點C為圓心,CA2為半徑的圓弧;
是以點C為圓心,CA2為半徑的圓弧;![]() 是以點A為圓心,AA3為半徑的圓弧,它們所對的圓心角都等于90°。繼續以點B、O、C、A為圓心按上述做法得到的曲線AA1A2A3A4A5……稱為“正方形的漸開線”,那么點A5的坐標是________,點A2018的坐標是_________
是以點A為圓心,AA3為半徑的圓弧,它們所對的圓心角都等于90°。繼續以點B、O、C、A為圓心按上述做法得到的曲線AA1A2A3A4A5……稱為“正方形的漸開線”,那么點A5的坐標是________,點A2018的坐標是_________

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,Rt△ABC的三個頂點分別是A(-3,2)、B(0,4)、C(0,2),
(1)畫出△ABC關于點C成中心對稱的△A1B1C;
(2)平移△ABC:若點A的對應點A2的坐標為(0,-4),畫出平移后對應的△A2B2C2;
(3)△A1B1C和△A2B2C2關于某一點成中心對稱,則對稱中心的坐標為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某“數學興趣小組”根據學習函數的經驗,對函數![]() 的圖象和性質進行了探究,探究過程如下,請補充完整:
的圖象和性質進行了探究,探究過程如下,請補充完整:
(1)自變量x的取值范圍是全體實數,x與y的幾組對應數值如下表:
x | … | -3 | - | -2 | -1 | 0 | 1 | 2 |
| 3 | … |
y | … | -2 | - | m | 2 | 1 | 2 | 1 | - | -2 | … |
其中m=____________;
(2)如圖,在平面直角坐標系xOy中,描出了以上表中各對對應值為坐標的點,根據描出的點,畫出該函數的圖象;

(3)根據函數圖象
①寫出該函數的一條性質_______________;
②直線![]() 經過點(-l,2),若關于x的方程
經過點(-l,2),若關于x的方程![]() 有4個互不相等的實數根,則b的取值范圍是__________________.
有4個互不相等的實數根,則b的取值范圍是__________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】人類的血型一般可分為A,B,AB,O型四種,寧波市中心血戰2015年共有8萬人無償獻血,血戰統計人員由電腦隨機選出20人,血型分別是:
O,A,O,B,O,A,A,AB,A,O,O,B,AB,B,O,A,O,B,O,A.
(1)請設計統計表分類統計這20人各類血型人數;
(2)若每位獻血者平均獻血200毫升,一年中寧波市各醫院O型血用血量約為6×106毫米,請你估計2015年這8萬人所獻的O型血是否夠用?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 在平面直角坐標系xOy中,O為坐標原點,四邊形OABC的頂點A在x軸的正半軸上,OA=4,OC=2,點P,點Q分別是邊BC,邊AB上的點,連結AC,PQ,點B1是點B關于PQ的對稱點.
(1)若四邊形OABC為長方形,如圖1,
①求點B的坐標;
②若BQ=BP,且點B1落在AC上,求點B1的坐標;
(2)若四邊形OABC為平行四邊形,如圖2,且OC⊥AC,過點B1作B1F∥x軸,與對角線AC,邊OC分別交于點E,點F.若B1E:B1F=1:3,點B1的橫坐標為m,求點B1的縱坐標(用含m的代數式表示).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com