
 如圖,C為線段BD上一點,BC=3,CD=2.△ABC、△ECD均為正三角形,AD交CE于F,則S△ACF:S△DEF的值為( )
如圖,C為線段BD上一點,BC=3,CD=2.△ABC、△ECD均為正三角形,AD交CE于F,則S△ACF:S△DEF的值為( ) 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:初中數學 來源: 題型:
 (2012•青田縣模擬)為了探索代數式
(2012•青田縣模擬)為了探索代數式| x2+1 |
| (8-x)2+25 |
| x2+1 |
| (8-x)2+25 |
| x2+1 |
| (8-x)2+25 |
| 4 |
| 3 |
| 4 |
| 3 |
| x2+4 |
| (12-x)2+9 |
查看答案和解析>>
科目:初中數學 來源: 題型:
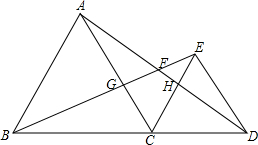 如圖,C為線段BD上一點(不與點B,D重合),在BD同側分別作正三角形ABC和正三角形CDE,AD與BE交于一點F,AD與CE交于點H,BE與AC交于點G.
如圖,C為線段BD上一點(不與點B,D重合),在BD同側分別作正三角形ABC和正三角形CDE,AD與BE交于一點F,AD與CE交于點H,BE與AC交于點G.查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com