
【題目】綜合與探究.
如圖1,拋物線y=![]() x2﹣
x2﹣![]() x﹣2與x軸交于A,B兩點,與y軸交于點C,經過點B的直線交y軸于點E(0,2).
x﹣2與x軸交于A,B兩點,與y軸交于點C,經過點B的直線交y軸于點E(0,2).
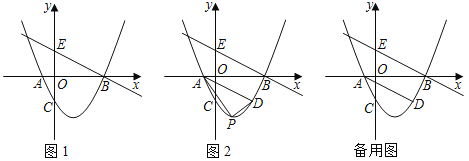
(1)求A,B,C三點的坐標及直線BE的解析式.
(2)如圖2,過點A作BE的平行線交拋物線于點D,點P是拋物線上位于線段AD下方的一個動點,連接PA,PD,求OAPD面積的最大值.
(3)若(2)中的點P為拋物線上一動點,在x軸上是否存在點Q,使得以A,D,P,Q為頂點的四邊形是平行四邊形?若存在,請直接寫出點Q的坐標;若不存在,請說明理由.
【答案】(1)A(﹣1,0),B(4,0),C(0,﹣2);y=﹣![]() x+2;(2) 4;(3)存在;點Q的坐標為(2,0)或(﹣4,0)或(
x+2;(2) 4;(3)存在;點Q的坐標為(2,0)或(﹣4,0)或(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
(1)令y=0可求A與B點坐標,令x=0可求出C點的坐標;設直線BE的解析式為y=kx+b,將B(4,0)、E(0,2)代入解析式可求k與b的值;
(2)設AD的解析式為y=-![]() x+m,將A(-1,0)代入求出m,進而確定直線AD的解析式,再聯立
x+m,將A(-1,0)代入求出m,進而確定直線AD的解析式,再聯立 求出D點坐標,過點P作PF⊥x軸于點F,交AD于點N,過點D作DG⊥x軸于點G.則S△APD=S△APN+S△DPN=2PN,設P
求出D點坐標,過點P作PF⊥x軸于點F,交AD于點N,過點D作DG⊥x軸于點G.則S△APD=S△APN+S△DPN=2PN,設P![]() ,則N
,則N![]() ,求出PN=-
,求出PN=-![]() a2+a+
a2+a+![]() ,所以S△APD=-a2+2a+3=-(a-1)2+4,當a=1時,△APD的面積最大,最大值為4;
,所以S△APD=-a2+2a+3=-(a-1)2+4,當a=1時,△APD的面積最大,最大值為4;
(3)分兩種情況討論:①當PD與AQ為平行四邊形的對邊時,由PD=AQ=3,可求Q(2,0)或Q(-4,0);②當PD與AQ為平行四邊形的對角線時,先求出P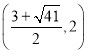 或P
或P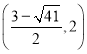 ,再求出PD的中點為
,再求出PD的中點為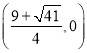 或
或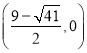 ,由平行四邊形對角線的性質可求Q
,由平行四邊形對角線的性質可求Q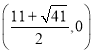 或Q
或Q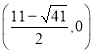 .
.
解:(1)令y=0,則![]() x2﹣
x2﹣![]() x﹣2=0,解得x=4或x=﹣1,
x﹣2=0,解得x=4或x=﹣1,
∴A(﹣1,0),B(4,0),
令x=0,則y=﹣2,∴C(0,﹣2),
設直線BE的解析式為y=kx+b,
將B(4,0)、E(0,2)代入得,![]() ,解得:
,解得: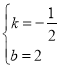 ,
,
∴y=﹣![]() x+2;
x+2;
(2)由題意可設AD的解析式為y=﹣![]() x+m,
x+m,
將A(﹣1,0)代入,得到m=﹣![]() ,
,
∴y=﹣![]() x﹣
x﹣![]() ,
,
聯立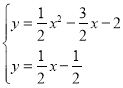 ,
,
解得:![]() ,
,![]() ,
,
∴D(3,﹣2),
過點P作PF⊥x軸于點F,交AD于點N,過點D作DG⊥x軸于點G.
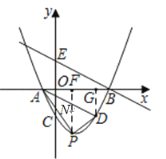
∴S△APD=S△APN+S△DPN=![]() PNAF+
PNAF+![]() PNFG=
PNFG=![]() PN(AF+FG)=
PN(AF+FG)=![]() PNAG=
PNAG=![]() ×4PN=2PN,
×4PN=2PN,
設P(a,﹣![]() a2﹣
a2﹣![]() a﹣2),則N(a,﹣
a﹣2),則N(a,﹣![]() a﹣
a﹣![]() ),
),
∴PN=﹣![]() a2+a+
a2+a+![]() ,
,
∴S△APD=﹣a2+2a+3=﹣(a﹣1)2+4,
∵﹣1<0,﹣1<a<3,
∴當a=1時,△APD的面積最大,最大值為4;
(3)存在;
①當PD與AQ為平行四邊形的對邊時,
∵AQ∥PD,AQ在x軸上,
∴P(0,﹣2),
∴PD=3,
∴AQ=3,
∵A(﹣1,0),
∴Q(2,0)或Q(﹣4,0);
②當PD與AQ為平行四邊形的對角線時,
PD與AQ的中點在x軸上,
∴P點的縱坐標為2,
∴P(![]() ,2)或P(
,2)或P(![]() ,2),
,2),
∴PD的中點為(![]() ,0)或(
,0)或(![]() ,0),
,0),
∵Q點與A點關于PD的中點對稱,
∴Q(![]() ,0)或Q(
,0)或Q(![]() ,0);
,0);
綜上所述:點Q的坐標為(2,0)或(﹣4,0)或(![]() ,0)或(
,0)或(![]() ,0).
,0).


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:初中數學 來源: 題型:
【題目】 “六一”前夕質監部門從某超市經銷的兒童玩具、童車和童裝中共抽查了300件兒童用品,以下是根據抽查結果繪制出的不完整的統計表和扇形圖;
類別 | 兒童玩具 | 童車 | 童裝 |
抽查件數 | 90 |

請根據上述統計表和扇形提供的信息,完成下列問題:
(1)分別補全上述統計表和統計圖;
(2)已知所抽查的兒童玩具、童車、童裝的合格率分別為90%、88%、80%,若從該超市的這三類兒童用品中隨機購買一件,買到合格品的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于點
軸分別交于點![]() ,
,![]() ,拋物線
,拋物線![]() 經過點
經過點![]() ,將點
,將點![]() 向右平移5個單位長度,得到點
向右平移5個單位長度,得到點![]() .
.
(1)求點![]() 的坐標;
的坐標;
(2)求拋物線的對稱軸;
(3)若拋物線與線段![]() 恰有一個公共點,結合函數圖象,求
恰有一個公共點,結合函數圖象,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
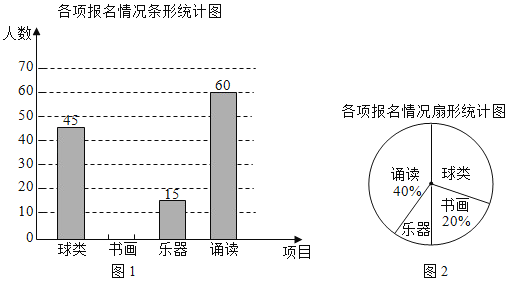
【題目】某校開展以“我們都是追夢人”為主題的校園文化節活動,活動分為球類、書畫、樂器、誦讀四項內容,要求每位學生參加其中的一項.校學生會為了解各項報名情況,隨機抽取了部分學生進行調查,并對調查結果進行了統計,繪制了如下統計圖(均不完整):
請解答以下問題:
(1)圖1中,“書畫”這一項的人數是 .
(2)圖2中,“樂器”這一項的百分比是 ,“球類”這一項所對應的扇形的圓心角度數是 .
(3)若該校共有2200名學生,請估計該校參加“誦讀”這一項的學生約有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
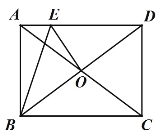
【題目】如圖,矩形 ABCD 的對角線 AC 與 BD 交于點 O,點 E 在 AD 上,且 DE=CD,連接 OE,BE, ABE ![]() ACB ,若 AE=2,則 OE 的長為___________.
ACB ,若 AE=2,則 OE 的長為___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
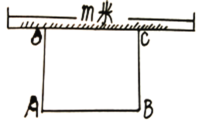
【題目】為配合我市“創建全國文明城市”某單位計劃在一塊矩形空地上修建綠色植物園(如圖所示),其中邊靠墻(墻長為![]() 米),另外三邊用總長36米的材料圍成.若
米),另外三邊用總長36米的材料圍成.若![]() 米,矩形
米,矩形![]() 的面積為
的面積為![]() 平方米.
平方米.
(1)求![]() 與
與![]() 的函數關系式;
的函數關系式;
(2)若矩形面積為160平方米,求![]() 的長.
的長.
(3)在(2)的前提下,墻長![]() 米對
米對![]() 的長有影響嗎?請詳細說明.
的長有影響嗎?請詳細說明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,設點P(x1,y1),Q(x2,y2)是圖形W上的任意兩點.
定義圖形W的測度面積:若|x1﹣x2|的最大值為m,|y1﹣y2|的最大值為n,則S=mn為圖形W的測度面積.
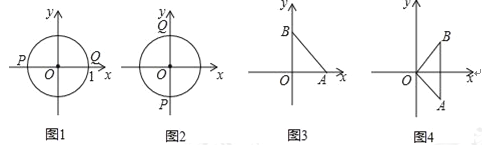
例如,若圖形W是半徑為1的⊙O,當P,Q分別是⊙O與x軸的交點時,如圖1,|x1﹣x2|取得最大值,且最大值m=2;當P,Q分別是⊙O與y軸的交點時,如圖2,|y1﹣y2|取得最大值,且最大值n=2.則圖形W的測度面積S=mn=4
(1)若圖形W是等腰直角三角形ABO,OA=OB=1.
①如圖3,當點A,B在坐標軸上時,它的測度面積S= ;
②如圖4,當AB⊥x軸時,它的測度面積S= ;
(2)若圖形W是一個邊長1的正方形ABCD,則此圖形的測度面積S的最大值為 ;
(3)若圖形W是一個邊長分別為3和4的矩形ABCD,求它的測度面積S的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com