
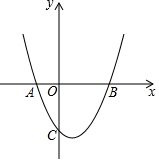
 如圖,拋物線y=x2-2x-3與x軸交于A、B兩點,與y軸交于點C.
如圖,拋物線y=x2-2x-3與x軸交于A、B兩點,與y軸交于點C.分析 (1)把C(0,-3)代入拋物線解析式可得k值,令y=0,可得A,B兩點的橫坐標;
(2)過M點作x軸的垂線,把四邊形ABMC分割成兩個直角三角形和一個直角梯形,求它們的面積和;
(3)設D(m,m2-2m-3),連接OD,把△BCD的面積轉化成求△BOC,△DOC,△DOB的面積的和差,求表達式的最大值.
解答 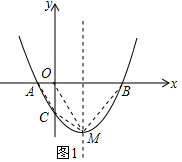 解:(1)在y=x2-2x-3中,
解:(1)在y=x2-2x-3中,
令y=0,
即x2-2x-3=0,
解得 x1=-1,x2=3.
令x=0,得y=-3,
∴A(-1,0),B(3,0),C(0,-3),
故答案是:(-1,0);(3,0);(0,-3);
(2)∵y=x2-2x-3=(x-1)2-4,
∴拋物線的頂點為M(1,-4).
如圖1,連接OM、AC、CM、MB.
則S△AOC=$\frac{3}{2}$,S△MOC=$\frac{3}{2}$,
S△MOB=6,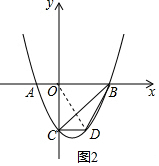
∴S四邊形ABMC=S△AOC+S△MOC+S△MOB=9;
(3)如圖2,設D(m,m2-2m-3),連接OD.
則0<m<3,m2-2m-3<0
∵△DOC的面積=$\frac{3}{2}$m,
△DOB的面積=-$\frac{3}{2}$(m2-2m-3),
∴S△BDC=S△DOC+S△DOB-S△BOC
=$\frac{3}{2}$m-$\frac{3}{2}$(m2-2m-3)-$\frac{1}{2}×$3×3=-$\frac{3}{2}$m2+$\frac{9}{2}$m=-$\frac{3}{2}$(m-$\frac{3}{2}$)2+$\frac{27}{8}$,
∴存在點D( $\frac{3}{2}$,-$\frac{15}{4}$),使△BCD的面積最大為 $\frac{27}{8}$.
點評 本題考查了待定系數法求二次函數解析式、二次函數圖象上點的坐標特征以及不規則圖形面積的求法等二次函數綜合題型.解答(2)題時,也可過點M作拋物線的對稱軸,將四邊形ABMC的面積轉化為求一個梯形與兩個直角三角形面積的和.


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:初中數學 來源: 題型:解答題
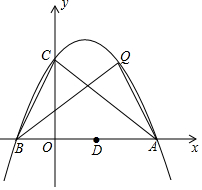 如圖,拋物線y=ax2-2ax+c(a≠0)與y軸相交于點C(0,4),與x軸相交于A、B兩點,點A的坐標為(4,0).
如圖,拋物線y=ax2-2ax+c(a≠0)與y軸相交于點C(0,4),與x軸相交于A、B兩點,點A的坐標為(4,0).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com