已知函數 y=(5m-3)x2-n+(n+m),
(1)當m,n為何值時是一次函數?
(2)當m,n為何值時,為正比例函數?
(3)當m,n為何值時,為反比例函數?
解:(1)當函數y=(5m-3)x
2-n+(m+n)是一次函數時,
2-n=1,且5m-3≠0,
解得,n=1,m≠

;
(2)當函數y=(5m-3)x
2-n+(m+n)是正比例函數時,
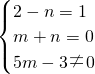
,
解得,n=1,m=-1.
(3)當函數y=(5m-3)x
2-n+(m+n)是反比例函數時,
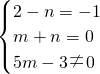
,
解得n=3,m=-3.
分析:(1)根據一次函數的定義知2-n=1,且5m-3≠0,據此可以求得m、n的值;
(2)根據正比例函數的定義知2-n=1,m+n=0,5m-3≠0,據此可以求得m、n的值;
(3)根據反比例函數的定義知2-n=-1,m+n=0,5m-3≠0,據此可以求得m、n的值.
點評:本題考查了一次函數、正比例函數、反比例函數的定義.關鍵是掌握正比例函數是一次函數的一種特殊形式以及三種函數的關系是形式.

 ;
;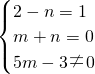 ,
,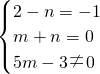 ,
,

 課堂練加測系列答案
課堂練加測系列答案 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案