
【題目】已知直線![]() 或
或![]() 與反比例函數
與反比例函數![]() 的圖象交于
的圖象交于![]() 、
、![]() 兩點,
兩點,![]() ,則
,則![]() 的值為__________.
的值為__________.
【答案】0或4或-4
【解析】
首先對一次函數進行分類討論,由于反比例函數![]() 的圖象在第一、三象限,所以①
的圖象在第一、三象限,所以①![]() 與反比例函數
與反比例函數![]() 交于
交于![]() ,
,![]() 兩點,此時根據
兩點,此時根據![]() ,以及直線
,以及直線![]() 與坐標軸的夾角為
與坐標軸的夾角為![]() ,可以求出
,可以求出![]() 兩點的坐標為
兩點的坐標為![]() ,
,![]() ,代入直線
,代入直線![]() 即可解出
即可解出![]() ;②
;②![]() 與反比例函數
與反比例函數![]() 交于
交于![]() ,
,![]() 兩點,此時還應再分兩種情況,i:
兩點,此時還應再分兩種情況,i:![]() ,設出
,設出![]() 的橫坐標為
的橫坐標為![]() ,則縱坐標為
,則縱坐標為![]() ,利用反比例函數的性質列出方程
,利用反比例函數的性質列出方程![]() ,解出
,解出![]() 即可求出
即可求出![]() 的值;ii:
的值;ii:![]() ,和上面同樣的方法即可求解;
,和上面同樣的方法即可求解;
因為直線![]() 或
或![]() 與反比例函數
與反比例函數![]() 的圖象交于
的圖象交于![]() ,
,![]() 兩點,①由于反比例函數
兩點,①由于反比例函數![]() 的圖象在第一、三象限,當
的圖象在第一、三象限,當![]() 與反比例函數
與反比例函數![]() 的圖象交于
的圖象交于![]() ,
,![]() 兩點,且
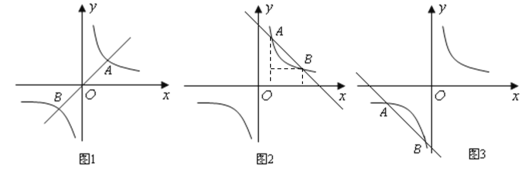
兩點,且![]() 時(如圖1),因為反比例函數
時(如圖1),因為反比例函數![]() 的圖象的兩支最接近的兩點
的圖象的兩支最接近的兩點![]() 與
與![]() 之間的距離為4,此時
之間的距離為4,此時![]() ;②當直線
;②當直線![]() 與反比例函數
與反比例函數![]() 的圖象交于
的圖象交于![]() ,
,![]() 兩點時,應分兩種情況:一是在圖2中,
兩點時,應分兩種情況:一是在圖2中,![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() ,則縱坐標為
,則縱坐標為![]() ,則有
,則有![]() ,解得
,解得![]() ,則有
,則有![]() 過點
過點![]() ,代入解析式中可得
,代入解析式中可得![]() ;同理,在圖3中,可求得
;同理,在圖3中,可求得![]() .
.
故答案是:0或4或-4


科目:初中數學 來源: 題型:
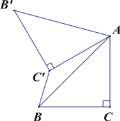
【題目】如圖 ,已知△ABC 中,∠C=90°,AC=BC=![]() ,將△ABC 繞點 A 順時針方向旋轉 60°得到△A′B′C′的位置,連接 C′B,則 C′B 的長為 ( )
,將△ABC 繞點 A 順時針方向旋轉 60°得到△A′B′C′的位置,連接 C′B,則 C′B 的長為 ( )
A.2-![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線y=![]() x+4與x軸、y軸分別交于點A和點B,點C,D分別為線段AB,OB的中點,點P為OA上一動點,PC+PD值最小時點P的坐標為.
x+4與x軸、y軸分別交于點A和點B,點C,D分別為線段AB,OB的中點,點P為OA上一動點,PC+PD值最小時點P的坐標為.

A. (-3,0) B. (-6,0) C. (-![]() ,0) D. (-
,0) D. (-![]() ,0)
,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩個小組同時從甲地出發,勻速步行到乙地,甲乙兩地相距7500米.第一組的步行速度是第二組的1.2倍,并且比第二組早15分鐘到達乙地.設第二組的步行速度為![]() 千米/小時,根據題意可列方程________.
千米/小時,根據題意可列方程________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() 是
是![]() 延長線上的定點,
延長線上的定點,![]() 為
為![]() 邊上的一個動點,連接
邊上的一個動點,連接![]() ,將射線
,將射線![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() ,交射線
,交射線![]() 于點
于點![]() ,連接
,連接![]() .
.
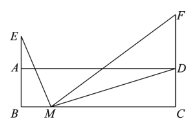
小東根據學習函數的經驗,對線段![]() 的長度之間的關系進行了探究.
的長度之間的關系進行了探究.
下面是小東探究的過程,請補充完整:
(1)對于點![]() 在
在![]() 上的不同位置,畫圖、測量,得到了線段
上的不同位置,畫圖、測量,得到了線段![]() 的長度的幾組值,如下表:
的長度的幾組值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | |
| 0.00 | 0.53 | 1.00 | 1.69 | 2.17 | 2.96 | 3.46 | 3.79 | 4.00 |
| 0.00 | 1.00 | 1.74 | 2.49 | 2.69 | 2.21 | 1.14 | 0.00 | 1.00 |
| 4.12 | 3.61 | 3.16 | 2.52 | 2.09 | 1.44 | 1.14 | 1.02 | 1.00 |
在![]() 的長度這三個量中,確定_____的長度是自變量,_____的長度和_____的長度都是這個自變量的函數;
的長度這三個量中,確定_____的長度是自變量,_____的長度和_____的長度都是這個自變量的函數;
(2)在同一平面直角坐標系![]() 中,畫出(1)中所確定的兩個函數的圖象;
中,畫出(1)中所確定的兩個函數的圖象;
(3)結合畫出的函數圖象,解決問題:當![]() 時,
時,![]() 的長度約為________
的長度約為________![]() .
.

查看答案和解析>>
科目:初中數學 來源: 題型:
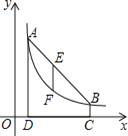
【題目】如圖,點![]() ,
,![]() 在反比例函數
在反比例函數![]() 的圖象上,
的圖象上,![]() 軸于點
軸于點![]() ,
,![]() 軸于點
軸于點![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的值和反比例函數的解析式;
的值和反比例函數的解析式;
(2)連接![]() ,
,![]() 是線段
是線段![]() 上一點,過點
上一點,過點![]() 作
作![]() 軸的垂線,交反比例函數圖象于點
軸的垂線,交反比例函數圖象于點![]() ,若
,若![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點(點
兩點(點![]() 在點
在點![]() 的右側),與
的右側),與![]() 軸交于點
軸交于點![]() ,已知
,已知![]() ,
,![]() 兩點的坐標分別為
兩點的坐標分別為![]() ,
,![]()
(1)求拋物線的表達式;
(2)一動點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 以每秒1個單位長度的速度向點
以每秒1個單位長度的速度向點![]() 運動,同時點
運動,同時點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 以每秒1個單位長度的速度向點
以每秒1個單位長度的速度向點![]() 運動,當點
運動,當點![]() 運動到點
運動到點![]() 時,點
時,點![]() 隨之停止運動.設運動時間為
隨之停止運動.設運動時間為![]() 秒,當
秒,當![]() 為何值時以
為何值時以![]() 、
、![]() 、
、![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?
相似?
(3)若點![]() 是
是![]() 軸上一動點,點
軸上一動點,點![]() 是拋物線上一動點,試判斷是否存在以點
是拋物線上一動點,試判斷是否存在以點![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形是平行四邊形.若存在,請直接寫出點
為頂點的四邊形是平行四邊形.若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
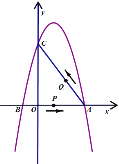
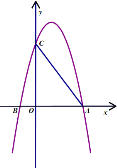


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖 1,在平行四邊形![]() 中,點
中,點![]() 是對角線
是對角線![]() 的中點,過點
的中點,過點![]() 的直線分別交
的直線分別交![]() 于點
于點![]() 若平行四邊形
若平行四邊形![]() 的面積是 8,則四邊形
的面積是 8,則四邊形![]() 的面積是___________ .
的面積是___________ .
(2)如圖 2,在菱形![]() 中,對角線相交于點 O,過點 O 的直線分別交
中,對角線相交于點 O,過點 O 的直線分別交![]() 于點
于點![]() ,若
,若![]() ,求四邊形
,求四邊形![]() 的面積.
的面積.
(3)如圖 3,在![]() 中,
中,![]() ,延長
,延長![]() 到點
到點![]() ,使
,使![]() ,連結
,連結![]() ,若
,若![]() ,則
,則![]() 的面積是____________ .
的面積是____________ .
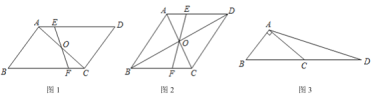
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場用2500元購進A、B兩種新型節能臺燈共50盞,這兩種臺燈的進價、標價如下表所示.
類型 價格 | A型 | B型 |
進價(元/盞) | 40 | 65 |
標價(元/盞) | 60 | 100 |
(1)這兩種臺燈各購進多少盞?
(2)在每種臺燈銷售利潤不變的情況下,若該商場計劃銷售這批臺燈的總利潤至少為1400元,問至少需購進B種臺燈多少盞?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com