
如圖,頂點為A的拋物線y=a(x+2)2﹣4交x軸于點B(1,0),連接AB,過原點O作射線OM∥AB,過點A作AD∥x軸交OM于點D,點C為拋物線與x軸的另一個交點,連接CD.
(1)求拋物線的解析式,直線AB的解析式;
(2)若動點P從點O出發,以每秒1個單位長度的速度沿線段OD向點D運動,同時動點Q從點C出發,以每秒2個單位長度的速度沿線段CO向點O運動,當其中一個點停止運動時另一個點也隨之停止運動.
問題一:當t為何值時,△OPQ為等腰三角形?
問題二:當t為何值時,四邊形CDPQ的面積最小?并求此時PQ的長.


解:(1)由頂點為A的拋物線y=a(x+2)2﹣4交x軸于點B(1,0)可得:
0=a(1+2)2﹣4,解得:a=
 ,∴拋物線的解析式:
,∴拋物線的解析式: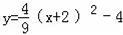
 ,頂點A(﹣2,﹣4),
,頂點A(﹣2,﹣4),
設直線AB:y=bx+k,帶入點A,B兩點坐標得:
 ,解得:
,解得:
 ,
,
∴直線AB的解析式:y=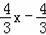
 ,
,
(2)如圖:


∵OD∥AB,所以得直線OD:y=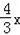
 ,
,
∵AD∥x軸,解得點D(﹣3,﹣4),
解得OD=5,tan∠COD=
 ,sin∠COD=
,sin∠COD=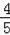
 ,cos∠COD=
,cos∠COD=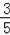
 ,
,
把y=0帶入拋物線解析式得:0=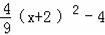
 ,
,
解得:x=1,或x=﹣5,所以點C(﹣5,0),∴OC=5,
由2t≤5,得t≤2.5,OP=t,OQ=5﹣2t,
當OP=OQ時,有:t=5﹣2t,解得t=
 ,
,
當OQ=QP時,有:t=2(5﹣2t)×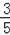
 ,解得t=
,解得t=
 ,
,
當QP=OP時,有:5﹣2t=2t×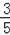
 ,解得t=
,解得t=
 ,
,
綜上所述,當t為
 ,
,
 ,
,
 時,△OPQ為等腰三角形;
時,△OPQ為等腰三角形;
四邊形CDPQ的面積=S△QCD﹣S△OQP=
 ×5×4﹣
×5×4﹣
 ×(5﹣2t)×t×
×(5﹣2t)×t×
 =
=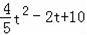
 ,
,
所以當t=
 =
=
 時,四邊形CDPQ的面積有最小值,
時,四邊形CDPQ的面積有最小值,
此時,OQ=
 ,OP=
,OP=
 ,sin∠COD=
,sin∠COD=
 ,cos∠COD=
,cos∠COD=
 ,可求得PQ=
,可求得PQ=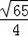
 .
.


科目:初中數學 來源: 題型:
為了提高學生書寫漢字的能力,增強保護漢字的意識,我市舉辦了首屆“漢字聽寫大賽”,經選拔后有50名學生參加決賽,這50名學生同時聽寫50個漢字,若每正確聽寫出一個漢字得1分,根據測試成績繪制出部分頻數分布表和部分頻數分布直方圖如圖表:


請結合圖表完成下列各題:
(1)求表中a的值;
(2)請把頻數分布直方圖補充完整;
(3)若測試成績不低于40分為優秀,則本次測試的優秀率是多少?
(4)第5組10名同學中,有4名男同學,現將這10名同學平均分成兩組進行對抗練習,且4名男同學每組分兩人,求小宇與小強兩名男同學能分在同一組的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com