【題目】已知：△ABC在坐標平面內，三個頂點的坐標分別為A（0，3），B（3，4），C（2，2）.（正方形網格中， 每個小正方形的邊長是1個單位長度）
（1）畫出△ABC向下平移4個單位得到的△A1B1C1，并直接寫出C1點的坐標；
（2）以點B為位似中心，在網格中畫出△A2BC2，使△A2BC2與△ABC位似，且位似比為2︰1，并直接寫出C2點的坐標及△A2BC2的面積．
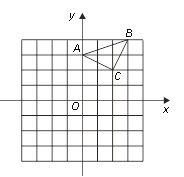
【答案】（1）畫圖見解析，C1(2，－2)；（2）畫圖見解析，C2（1,0） △A2BC2的面積等于10
【解析】分析：（1）根據網格結構，找出點A、B、C向下平移4個單位的對應點
、
、
的位置，然后順次連接即可，再根據平面直角坐標系寫出點的坐標；（2）延長BA到
使A=AB，延長BC到
，使C=BC，然后連接A2C2即可，再根據平面直角坐標系寫出點的坐標，利用△B所在的矩形的面積減去四周三個小直角三角形的面積，列式計算即可得解．
本題解析：（1）如圖，△A1B1C1即為所求，C1(2，－2)
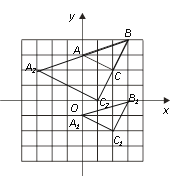
(2)如圖,△B為所求, (1,0)，
△B 的面積：
6×4
×2×6×2×4×2×4=24644=2414=10，
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】廣州火車南站廣場計劃在廣場內種植A，B兩種花木共 6600棵，若A花木數量是B花木數量的2倍少600棵．
（1）A，B兩種花木的數量分別是多少棵？
（2）如果園林處安排26人同時種植這兩種花木，每人每天能種植A花木60棵或B花木40棵，應分別安排多少人種植A花木和B花木，才能確保同時完成各自的任務？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法正確的是（ ）
A. 經過一點有且只有一條直線與已知直線平行
B. 直線外一點到這條直線的垂線段，叫做點到直線的距離
C. 同一平面內，不相交的兩條直線是平行線
D. “相等的角是對頂角”是真命題
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某海灘景區門票價格為80元/人，景區為吸引游客，對門票價格進行動態管理，非節假日打a折，節假日期間，10人以下(包括10人)不打折，10人以上超過10人的部分打b折，設游客為x人，門票費用為y元，非節假日門票費用y1(元)及節假日門票費用y2(元)與游客x(人)之間的函數關系如圖所示．
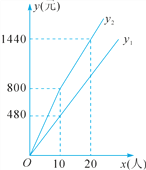
根據圖象，回答下列問題：
(1)a＝ ，b＝__ __．
(2)直接寫出y1，y2與x之間的函數表達式．
(3)導游小王6月10日(非節假日)帶A旅游團，6月20日(端午節)帶B旅游團到該海灘景區旅游，兩團共計50人，兩次共付門票費用3040元，求A，B兩個旅游團各有多少人.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知等腰三角形ABC的底角為30°，以BC為直徑的⊙O與底邊AB交于點D，過D作DE⊥AC，垂足為E．
（1）證明：DE為⊙O的切線；
（2）連接OE，若BC=4，求△OEC的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知在Rt△ABC中，∠C=900，AD是∠BAC的角分線.
（1）以AB上的一點O為圓心，AD為弦在圖中作出⊙O．（不寫作法，保留作圖痕跡）；
（2）試判斷直線BC與⊙O的位置關系，并證明你的結論；
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明新家裝修，在裝修客廳時，購進彩色地磚和單色地磚共100塊，共花費5600元．已知彩色地磚的單價是80元/塊，單色地磚的單價是40元/塊．
（1）兩種型號的地磚各采購了多少塊？
（2）如果廚房也要鋪設這兩種型號的地磚共60塊，且采購地磚的費用不超過3200元，那么彩色地磚最多能采購多少塊？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，拋物線y=ax2+
x+c過點A（0，4）和C（8，0），P（t，0）是x軸正半軸上的一個動點，M是線段AP的中點，將線段MP繞點P順時針旋轉90°得線段PB．過點B作x軸的垂線、過點A作y軸的垂線，兩直線相交于點D．
（1）求此拋物線的對稱軸；
（2）當t為何值時，點D落在拋物線上？
（3）是否存在t，使得以A、B、D為頂點的三角形與△PEB相似？若存在，求此時t的值；若不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com