
【題目】先閱讀下列材料,再解答下列問題:
題:分解因式:![]()
解:將“![]() ”看成整體,設
”看成整體,設![]() ,則原式=
,則原式=![]()
![]()
再將“![]() ”還原,得原式=
”還原,得原式=![]() .
.
上述解題用到的是“整體思想”,“整體思想”是數學解題中常用的一種思想方法,請你仿照上面的方法解答下列問題:
(1)因式分解:![]() ;
;![]() .
.
(2)因式分解:![]() ;
;![]() .
.
(3)求證:若![]() 為正整數,則式子
為正整數,則式子![]() 的值一定是某一個正整數的平方.
的值一定是某一個正整數的平方.
【答案】(1)![]() ;
;![]() .(2)
.(2)![]() ;
;![]() ;(3)證明見解析.
;(3)證明見解析.
【解析】
(1)把(2a+b),(3a+2b),(2a+3b)分別看作一個整體,直接利用平方差公式因式分解即可;
(2)把(x-y)看作一個整體,直接利用完全平方公式因式分解即可;把(a+b) 看作一個整體,代入后利用完全平方公式因式分解即可;
(3)將原式轉化為(n2+3n)[(n+1)(n+2)]+1,進一步整理為(n2+3n+1)2,根據n為正整數得到n2+3n+1也為正整數,從而說明原式是整數的平方.
(1)因式分解:![]()
![]() =
=![]() ;
;
![]()
![]()
=![]()
=![]() .
.
(2)因式分解:![]() (x-y+1)2;
(x-y+1)2;
令A=a+b,則原式變為A(A-4)+4=A2-4A+4=(A-2)2,
故(a+b)(a+b-4)+4=(a+b-2)2.
(3) (n+1)(n+2)(n2+3n)+1
=(n2+3n)[(n+1)(n+2)]+1
=(n2+3n)(n2+3n+2)+1
=(n2+3n)2+2(n2+3n)+1
=(n2+3n+1)2,
∵n為正整數,
∴n2+3n+1也為正整數,
∴代數式(n+1)(n+2)(n2+3n)+1的值一定是某一個整數的平方.


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:初中數學 來源: 題型:
【題目】如圖,點A的坐標為(0,1),點B是x軸正半軸上的一動點,以AB為邊作等腰Rt△ABC,使∠BAC=90°,設點B的橫坐標為x,設點C的縱坐標為y,能表示y與x的函數關系的圖象大致是( )
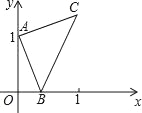
A. 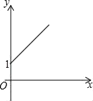 B.
B. 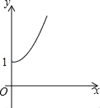 C.
C. 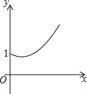 D.
D. 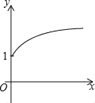
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列解題過程:
計算:1+5+52+53+…+524+525的值.
解:設S=1+5+52+53+…+524+525,(1)
則5S=5+52+53+…+525+526(2)
(2)﹣(1),得4S=526﹣1
S=![]()
通過閱讀,你一定學會了一種解決問題的方法,請用你學到的方法計算:
(1)1+3+32+33+…+39+310
(2)1+x+x2+x3+…+x99+x100.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】操作探究:已知在紙面上有一數軸(如圖所示),
![]()
(1)折疊紙面,使表示的點1與-1重合,則-2表示的點與 表示的點重合;
(2)折疊紙面,使-1表示的點與3表示的點重合,回答以下問題:
① 5表示的點與數 表示的點重合;
②![]() 表示的點與數 表示的點重合;
表示的點與數 表示的點重合;
③若數軸上A、B兩點之間距離為9(A在B的左側),且A、B兩點經折疊后重合,此時點A表示的數是 、點B表示的數是 .
(3)已知在數軸上點A表示的數是a,點A移動4個單位,此時點A表示的數和a是互為相反數,求a的值。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,數軸上,點A的初始位置表示的數為1,現點A做如下移動;第1次點A向左移動3個單位長度至點![]() ,第2次從點
,第2次從點![]() 向右移動6個單位長度至點
向右移動6個單位長度至點![]() ,第3次從點
,第3次從點![]() 向左移動9個單位長度至點
向左移動9個單位長度至點![]() ,…,按照這種移動方式進行下去,如果點
,…,按照這種移動方式進行下去,如果點![]() 與原點的距離不小于20,那么n的最小值是________.
與原點的距離不小于20,那么n的最小值是________.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
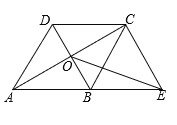
【題目】在四邊形ABCD中,AB∥DC,AB=AD,對角線AC,BD交于點O,AC平分∠BAD,過點C作CE∥DB交AB的延長線于點E,連接OE.
(1)求證:四邊形ABCD是菱形;
(2)若∠DAB=60°,且AB=4,求OE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
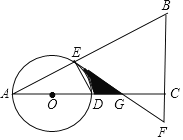
【題目】如圖,在△ABC中,∠ACB=90°,O是邊AC上一點,以O為圓心,OA為半徑的圓分別交AB,AC于點E,D,在BC的延長線上取點F,使得BF=EF,EF與AC交于點G.
(1)試判斷直線EF與⊙O的位置關系,并說明理由;
(2)若OA=2,∠A=30°,求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面上有四個點 A、B、C、D,根據下列語句畫圖:
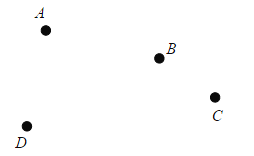
(1)畫直線 AB;
(2)作射線 BC;
(3)畫線段 CD;
(4)連接 DA 并延長,請使用直尺和圓規在線段 DA 的延長線上作線段 DE,使得 DE=2AD;
(5)數數看,此時圖中共有 條線段,以 A 為端點的射線共有 條.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某檢修小組乘一輛汽車沿東西方向方向檢修路,約定向東走為正,某天從![]() 地出發到收工時行走記錄(單位:
地出發到收工時行走記錄(單位:![]() ):
):![]() ,求:
,求:
(1)收工時檢修小組在![]() 地的在哪一邊,距
地的在哪一邊,距![]() 地多遠?
地多遠?
(2)若汽車耗油![]() 升/每千米,開工時儲存
升/每千米,開工時儲存![]() 升汽油,用到收工時中途是否需要加油;
升汽油,用到收工時中途是否需要加油;
(3)若加油,最少加多少升才能保證收工后返回![]() 地?若不需要加油,到收工時,還剩多少升汽油?
地?若不需要加油,到收工時,還剩多少升汽油?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com