久久久久久久一区,欧美日韩免费看,午夜影院男女

精英家教網 > 初中數學 > 題目詳情

【題目】某超市計劃經銷一些特產，經銷前，圍繞“A：王高虎頭雞，B：羊口咸蟹子，C：桂河芹菜，D：巨淀湖咸鴨蛋”四種特產，在全市范圍內隨機抽取了部分市民進行問卷調查：“我最喜歡的特產是什么？”（必選且只選一種）．現將調查結果整理后，繪制成如圖所示的不完整的扇形統(tǒng)計圖和條形統(tǒng)計圖．

(1)請補全扇形統(tǒng)計圖和條形統(tǒng)計圖；

(2)若全市有110萬市民，估計全市最喜歡“羊口咸蟹子”的市民約有多少萬人？

(3)在一個不透明的口袋中有四個分別寫上四種特產標記A、B、C、D的小球（除標記外完全相同），隨機摸出一個小球然后放回，混合搖勻后，再隨機摸出一個小球，則兩次都摸到A的概率是多少？寫出分析計算過程.

【答案】（1）補圖見解析；

（2）最喜歡“羊口咸蟹子”的市民約有45.1萬人；

（3）兩次都摸到A的概率是，分析過程見解析.

【解析】試題分析：（1）先根據條形圖中A的人數及扇形圖中A所占的百分比求出被調查的人數，然后根據相關數據通過計算即可得；

（2）用全市人口×“羊口咸蟹子”所占的比例即可得；

（3）畫樹狀圖或列表即可得.

試題解析：（1）被抽查的總人數：290÷29%=1000，

B的人數：1000﹣290﹣180﹣120=410，

C所占的百分比：180÷1000=18%；

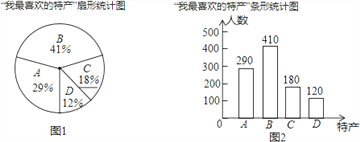
（2）110×41%=45.1（萬人），

（3）根據題意作出樹狀圖如下：

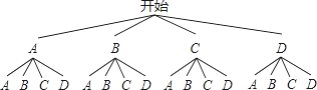
一共有16種情況，兩次都摸到“A”的有1種情況，

所以P（A，A）=．

故答案為：．

練習冊系列答案

本土寒假云南人民出版社系列答案

寒假作業(yè)南方日報出版社系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：初中數學 來源： 題型：

【題目】（提出問題）課間，一位同學拿著方格本遇人便問：“如圖所示，在邊長為1的小正方形組成的網格中，點A、B、C都是格點，如何證明點A、B、C在同一直線上呢？”

（分析問題）一時間，大家議論開了. 同學甲說：“可以利用代數方法，建立平面直角坐標系，利用函數的知識解決”，同學乙說：“也可以利用幾何方法…”同學丙說：“我還有其他的幾何證法”……

（解決問題）請你用兩種方法解決問題

方法一（用代數方法）：

方法二（用幾何方法）：

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖，在ABCD中，DE⊥AB，BF⊥CD，垂足分別為E，F．

（1）求證：△ADE≌△CBF；

（2）求證：四邊形BFDE為矩形．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖，在中，，點到兩邊的距離相等，且．

（1）先用尺規(guī)作出符合要求的點（保留作圖痕跡，不需要寫作法），然后判斷△ABP的形狀，并說明理由；

（2）設，，試用、的代數式表示的周長和面積；

（3）設與交于點，試探索當邊、的長度變化時，的值是否發(fā)生變化，若不變，試求出這個不變的值，若變化，試說明理由．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖，矩形 ABCD 的對角線 AC 與 BD 相交于點 O,CE∥BD, DE∥AC , AD＝2, DE＝2,則四邊形 OCED 的面積為（　　）

A. 2 B. 4 C. 4 D. 8

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】在平面直角坐標系中，有兩條拋物線關于x軸對稱，且它們的頂點相距6個單位長度，若其中一條拋物線的函數表達式為y＝﹣x2+4x+2m，則m的值是（　　）

A.B.C.1D.或

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】（1）問題感知如圖1，在△ABC中，∠C＝90°，且AC＝BC，點P是邊AC的中點，連接BP，將線段PB繞點P順時針旋轉90°到線段PD．連接AD．過點P作PE∥AB交BC于點E，則圖中與△BEP全等的三角形是　　，∠BAD＝　　°；

（2）問題拓展如圖2，在△ABC中，AC＝BC＝AB，點P是CA延長線上一點，連接BP，將線段PB繞點P順時針旋轉到線段PD，使得∠BPD＝∠C，連接AD，則線段CP與AD之間存在的數量關系為CP＝AD，請給予證明；

（3）問題解決如圖3，在△ABC中，AC＝BC＝AB＝2，點P在直線AC上，且∠APB＝30°，將線段PB繞點P順時針旋轉60°到線段PD，連接AD，請直接寫出△ADP的周長．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】武警戰(zhàn)士乘一沖鋒舟從地逆流而上，前往地營救受困群眾，途經地時，由所攜帶的救生艇將地受困群眾運回地，沖鋒舟繼續(xù)前進，到地接到群眾后立刻返回地，途中曾與救生艇相遇．沖鋒舟和救生艇距地的距離（千米）和沖鋒舟出發(fā)后所用時間（分）之間的函數圖象如圖所示．假設營救群眾的時間忽略不計，水流速度和沖鋒舟在靜水中的速度不變．