
【題目】已知△ABC中,∠BAC=90°,AB=AC.
(1)如圖,D為AC上任一點,連接BD,過A點作BD的垂線交過C點與AB平行的直線CE于點E.求證:BD=AE.
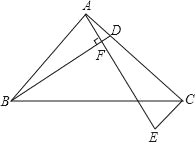
(2)若點D在AC的延長線上,如圖,其他條件同(1),請畫出此時的圖形,并猜想BD與AE是否仍然相等?說明你的理由.
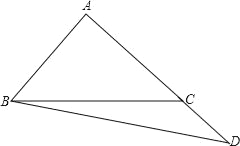
【答案】證明:(1)∵AB∥CE,
∴∠BAF=∠AEC,∠BAC+∠ACE=180°,
∵∠BAC=90°,
∴∠ACE=90°,
∵AF⊥BD,
∴∠ABD+∠BAF=90°,∠EAC+∠BAF=90°,
∴∠ABD=∠CAE
在△ABD和△CAE中,
AB="AC" ∠BAC=∠ACE ∠AEC=∠ABD ∴△ABD≌△CAE(AAS)
∴BD=AE.
(2)BD與AE仍然相等,
證明:過點C作AB∥CE,過點A作AE⊥BD于點F,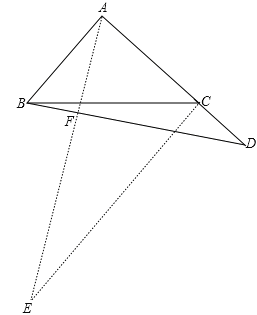
∵AB∥CE,
∴∠BAF=∠AEC,∠BAC+∠ACE=180°,
∵∠BAC=90°,
∴∠ACE=90°,
,∵AF⊥BD,
∴∠ABD+∠BAF=90°,∠EAC+∠BAF=90°,
∴∠ABD=∠CAE
在△ABD和△CAE中,
AB="AC" ∠BAC=∠ACE ∠AEC=∠ABD
∴△ABD≌△CAE(AAS)
∴BD=AE.
【解析】
(1)先證∠ABD=∠CAE,再證△ABD≌△CAE即可得出答案.
(2)根據題意畫出圖形,然后可根據△ABD≌△ACE得出結論


科目:初中數學 來源: 題型:
【題目】如圖,過ABCD的對角線BD上一點M分別作平行四邊形兩邊的平行線EF與GH,那么圖中的AEMG的面積S1與HCFM的面積S2的大小關系是( )
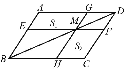
A. S1=S2 B. S1>S2 C. S1<S2 D. 不能確定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我校50名學生在某一天調查了75戶家庭丟棄塑料袋的情況,統計結果如下表:

根據上表回答下列問題:
(1)這天,一個家庭一天最多丟棄________個塑料袋.
(2)這天,丟棄3個塑料袋的家庭戶數占總戶數的________.
(3)該校所在的居民區共有居民0.8萬戶,則該區一天丟棄的塑料袋有多少個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用1塊A型鋼板可制成2塊C型鋼板、1塊D型鋼板;用1塊B型鋼板可制成1塊C型鋼板、2塊D型鋼板.
(1)現需150塊C型鋼板、180塊D型鋼板,則怡好用A型、B型鋼板各多少塊?
(2)若A、B型鋼板共100塊,現需C型鋼板至多150塊,D型鋼板不超過170塊,共有幾種方案?
(3)若需C型鋼板80塊,D型鋼板不多于45塊(A型、B型鋼板都要使用).求A、B型鋼板各需多少塊?
查看答案和解析>>
科目:初中數學 來源: 題型:
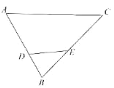
【題目】尺規作圖(不用寫出作法,保留作圖痕跡):
(1)在 DE 的上方,求作![]() FDE,使得
FDE,使得![]() FDE≌
FDE≌![]() BDE;
BDE;
(2)若∠B=50°,則∠ADF+∠CEF= °.
查看答案和解析>>
科目:初中數學 來源: 題型:
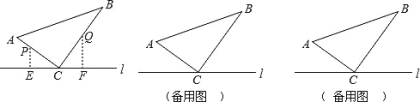
【題目】如圖,![]() ABC 中,∠ACB=90°,AC=6cm,BC=8cm,點 P 從 A 點出發沿 A-C-B 路徑向終點運動,終點為 B點;點 Q 從 B 點出發沿 B-C-A 路徑向終點運動,終點為 A 點,點 P 和 Q 分別以 1cm/s 和 xcm / s 的運動速度 同時開始運動,兩點都要到相應的終點時才能停止運動,在某時刻,分別過 P 和 Q 作 PE⊥ l 于 E,QF⊥ l 于 F.
ABC 中,∠ACB=90°,AC=6cm,BC=8cm,點 P 從 A 點出發沿 A-C-B 路徑向終點運動,終點為 B點;點 Q 從 B 點出發沿 B-C-A 路徑向終點運動,終點為 A 點,點 P 和 Q 分別以 1cm/s 和 xcm / s 的運動速度 同時開始運動,兩點都要到相應的終點時才能停止運動,在某時刻,分別過 P 和 Q 作 PE⊥ l 于 E,QF⊥ l 于 F.
(1)如圖,當 x 2 時,設點 P 運動時間為 ts ,當點 P 在 AC 上,點 Q 在 BC 上時:
①用含 t 的式子表示 CP 和 CQ,則 CP= cm,CQ= cm;
②當 t 2 時,![]() PEC 與
PEC 與![]() QFC 全等嗎?并說明理由;
QFC 全等嗎?并說明理由;
(2)請問:當 x 3 時,![]() PEC 與
PEC 與![]() QFC 有沒有可能全等?若能,直接寫出符合條件的 t 的值;若不能,請說明 理由。
QFC 有沒有可能全等?若能,直接寫出符合條件的 t 的值;若不能,請說明 理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com