
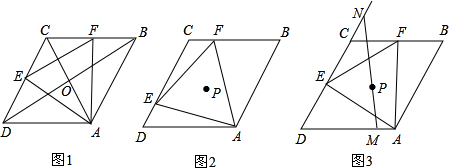
分析 (1)首先分別連接OE、0F,由四邊形ABCD是菱形,即可得AC⊥BD,BD平分∠ADC.AD=DC=BC,又由E、F分別為DC、CB中點,即可證得0E=OF=OA,則可得點O即為△AEF的外心;
(2)①首先分別連接PE、PA,過點P分別作PI⊥CD于I,PJ⊥AD于J,即可求得∠IPJ的度數(shù),又由點P是等邊△AEF的外心,易證得△PIE≌△PJA,可得PI=PJ,即點P在∠ADC的平分線上,即點P落在直線DB上.
②當AE⊥DC時.△AEF面積最小,此時點E、F分別為DC、CB中點.連接BD、AC交于點P,由(1)可得點P即為△AEF的外心.由△GBP∽△MDP,即可$\frac{1}{DM}+\frac{1}{DN}$為定值2.
解答 (1)證明:如圖①,分別連接OE、0F,
∵四邊形ABCD是菱形,
∴AC⊥BD,BD平分∠ADC.AD=DC=BC,
∴∠COD=∠COB=∠AOD=90°.
∠ADO=$\frac{1}{2}$∠ADC=$\frac{1}{2}$×60°=30°,
又∵E、F分別為DC、CB中點,
∴OE=$\frac{1}{2}$CD,OF=$\frac{1}{2}$BC,AO=$\frac{1}{2}$AD,
∴0E=OF=OA,
∴點O即為△AEF的外心;
(2)解:①猜想:外心P一定落在直線DB上.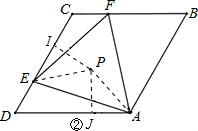 證明:如圖②,分別連接PE、PA,過點P分別作PI⊥CD于I,PJ⊥AD于J,
證明:如圖②,分別連接PE、PA,過點P分別作PI⊥CD于I,PJ⊥AD于J,
∴∠PIE=∠PJD=90°,
∵∠ADC=60°,
∴∠IPJ=360°-∠PIE-∠PJD-∠JDI=120°,
∵點P是等邊△AEF的外心,
∴∠EPA=120°,PE=PA,
∴∠IPJ=∠EPA,
∴∠IPE=∠JPA,
∴△PIE≌△PJA,
∴PI=PJ,
∴點P在∠ADC的平分線上,即點P落在直線DB上;
②$\frac{1}{DM}+\frac{1}{DN}$為定值2,
當AE⊥DC時.△AEF面積最小,
此時點E、F分別為DC、CB中點.
連接BD、AC交于點P,由(1)
可得點P在BD上,即為△AEF的外心,
如圖③.設MN交BC于點G,
設DM=x,DN=y(x≠0.y≠O),則CN=y-1,
∵BC∥DA,
∴△GBP≌△MDP,
∴BG=DM=x,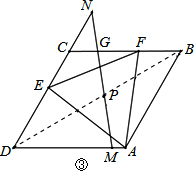
∴CG=1-x,
∵BC∥DA,
∴△NCG∽△NDM,
∴$\frac{CN}{DN}=\frac{CG}{DM}$,
∴$\frac{y-1}{y}$=$\frac{1-x}{x}$,
∴x+y=2xy,
∴$\frac{1}{x}$+$\frac{1}{y}$=2,
即$\frac{1}{DM}+\frac{1}{DN}$=2.
點評 此題考查了相似三角形的判定與性質,三角形的外心的判定與性質,以及菱形的性質等知識.此題綜合性很強,圖形也比較復雜,解題的關鍵是方程思想與數(shù)形結合思想的應用.


 名校通行證有效作業(yè)系列答案
名校通行證有效作業(yè)系列答案科目:初中數(shù)學 來源: 題型:解答題
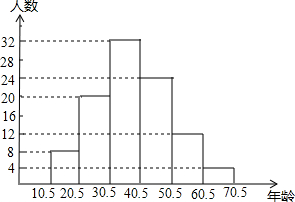 今年6月南博會在我市成功舉辦,吸引了眾多的國內外人士,期間,對六家大賓館、飯店中游客的年齡(年齡取整數(shù))進行了抽樣統(tǒng)計,經(jīng)整理后分成六組,并繪制成條形統(tǒng)計圖,如圖所示,請結合圖形回答下列問題:
今年6月南博會在我市成功舉辦,吸引了眾多的國內外人士,期間,對六家大賓館、飯店中游客的年齡(年齡取整數(shù))進行了抽樣統(tǒng)計,經(jīng)整理后分成六組,并繪制成條形統(tǒng)計圖,如圖所示,請結合圖形回答下列問題:查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題

| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
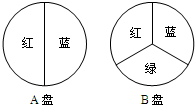 用如圖所示的A,B兩個轉盤進行“配紫色”游戲(紅色和藍色在一起配成了紫色).小亮和小剛同時轉動兩個轉盤,若配成紫色,小亮獲勝,否則小剛獲勝.這個游戲對雙方公平嗎?請你并說明理由.
用如圖所示的A,B兩個轉盤進行“配紫色”游戲(紅色和藍色在一起配成了紫色).小亮和小剛同時轉動兩個轉盤,若配成紫色,小亮獲勝,否則小剛獲勝.這個游戲對雙方公平嗎?請你并說明理由.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
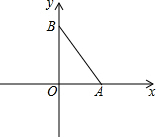 如圖,在平面直角坐標系中,A、B兩點分別在x軸、y軸上,OA=3,OB=4,連接AB.點P在平面內,若以點P、A、B為頂點的三角形與△AOB全等(點P與點O不重合),則點P的坐標為(3,4)或($\frac{96}{25}$,$\frac{72}{25}$)或(-$\frac{21}{25}$,$\frac{28}{25}$).
如圖,在平面直角坐標系中,A、B兩點分別在x軸、y軸上,OA=3,OB=4,連接AB.點P在平面內,若以點P、A、B為頂點的三角形與△AOB全等(點P與點O不重合),則點P的坐標為(3,4)或($\frac{96}{25}$,$\frac{72}{25}$)或(-$\frac{21}{25}$,$\frac{28}{25}$).查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com