
【題目】已知,點M為二次函數(shù)y=x2+2bx+3c圖象的頂點,一次函數(shù)y=kx﹣3(k>0)分別交x軸,y軸于點A,B.
(1)若b=1,c=1,判斷頂點M是否在直線y=2x+1上,并說明理由;
(2)若該二次函數(shù)圖象經過點C(1,﹣4),也經過點A,B,且滿足kx﹣3<x2+2bx+3c,求該一次函數(shù)解析式,并直接寫出自變量x的取值范圍;
(3)設點P坐標為(m,n)在二次函數(shù)y=x2+2bx+3c上,當﹣2≤m≤2時,b﹣24≤n≤2b+4,試問:當b≥2或b≤﹣2時,對于該二次函數(shù)中任意的自變量x,函數(shù)值y是否始終大于﹣40?請說明理由.
【答案】(1)M不在直線y=2x+1上,見解析;(2)y=x2﹣2x﹣3,x>3或x<0;(3)當b≥2或b≤﹣2時,對于該二次函數(shù)中任意的自變量x,函數(shù)值y始終大于﹣40
【解析】
(1)b=1,c=1時,y=x2+2x+3,求出M(﹣1,2),將點M(﹣1,2)代入y=2x+1驗證是否滿足即可;
(2)由題可知B(0,﹣3),C(1,﹣4),代入y=x2+2bx+3c得到b=﹣1,c=﹣1,求出A(![]() ,0),再將點A代入二次函數(shù)解析式得到
,0),再將點A代入二次函數(shù)解析式得到![]() ﹣
﹣![]() ﹣3=0,求得k=1;
﹣3=0,求得k=1;
(3)函數(shù)對稱軸為x=﹣b,①當﹣b≤﹣2時,即b≥2,此時b﹣24=4﹣4b+3c,則5b﹣3c=28,2b+4=4+4b+3c,則2b+3c=0,求得y=x2+8x﹣8=(x+4)2﹣24≥﹣24>﹣40;②當﹣b≥2時,即b≤﹣2,此時b﹣24=4+4b+3c,則3b+3c=﹣28,2b+4=4﹣4b+3c,則6b﹣3c=0,求得y=x2﹣![]() x﹣
x﹣![]() =(x﹣
=(x﹣![]() )2﹣
)2﹣![]() ≥﹣
≥﹣![]() >﹣40.
>﹣40.
解:(1)b=1,c=1時,y=x2+2x+3=(x+1)2+2,
∴M(﹣1,2),
將點M(﹣1,2)代入y=2x+1,則﹣1≠2,
∴M不在在直線y=2x+1上;
(2)∵B過一次函數(shù)y=kx-3且交于y軸,令x=0,解得y=-3,故B(0,-3).
∵B(0,﹣3),C(1,﹣4),過二次函數(shù)y=x2+2bx+3c.
代入得到:![]() ,解得:b=﹣1,c=﹣1,
,解得:b=﹣1,c=﹣1,
∴y=x2﹣2x﹣3,
∵A過y=kx-3并交x軸,令y=0,解得x=![]() ,故A(
,故A(![]() ,0),
,0),
∴![]() ﹣
﹣![]() ﹣3=0,
﹣3=0,
∴k=1或k=﹣3,
∵k>0,
∴k=1,
∴y=x﹣3,
∵x﹣3<x2﹣2x﹣3,
∴x>3或x<0;
(3)函數(shù)對稱軸為x=﹣b,
①當﹣b≤﹣2時,即b≥2,
此時b﹣24=4﹣4b+3c,則5b﹣3c=28,
2b+4=4+4b+3c,則2b+3c=0,
∴b=4,c=﹣![]() ,
,
∴y=x2+8x﹣8=(x+4)2﹣24≥﹣24>﹣40;
②當﹣b≥2時,即b≤﹣2,此時
b﹣24=4+4b+3c,則3b+3c=﹣28,
2b+4=4﹣4b+3c,則6b﹣3c=0,
∴b=﹣![]() ,c=﹣
,c=﹣![]() ,
,
∴y=x2﹣![]() x﹣
x﹣![]() =(x﹣
=(x﹣![]() )2﹣
)2﹣![]() ≥﹣
≥﹣![]() >﹣40;
>﹣40;
∴當b≥2或b≤﹣2時,對于該二次函數(shù)中任意的自變量x,函數(shù)值y始終大于﹣40.


科目:初中數(shù)學 來源: 題型:
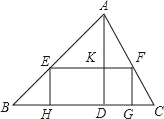
【題目】在銳角△ABC中,邊BC長為18,高AD長為12
(1)如圖,矩形EFCH的邊GH在BC邊上,其余兩個頂點E、F分別在AB、AC邊上,EF交AD于點K,求![]() 的值;
的值;
(2)設EH=x,矩形EFGH的面積為S,求S與x的函數(shù)關系式,并求S的最大值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】一根長40cm的金屬棒,欲將其截成x根7cm長的小段和y根9cm長的小段,剩余部分作廢料處理.若使廢料最少,則正整數(shù)x應為_.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系中,二次函數(shù)y=x2+bx+c的圖象與x軸交于A、B兩點,A點在原點的左側,B點的坐標為(3,0),與y軸交于點C(0,﹣3).
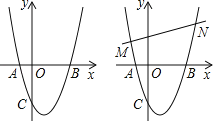
(1)求二次函數(shù)解析式;
(2)若點Q為拋物線上一點,且S△ABQ=![]() S△ACQ,求點Q的坐標;
S△ACQ,求點Q的坐標;
(3)若直線l:y=mx+n與拋物線有兩個交點M,N(M在N的左邊),P為拋物線上一動點(不與M,N重合).過P作PH平行于y軸交直線l于點H,若![]() =5,求m的值.
=5,求m的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線y=x2+mx交x軸的負半軸于點A.點B是y軸正半軸上一點,點A關于點B的對稱點A′恰好落在拋物線上.過點A′作x軸的平行線交拋物線于另一點C.若點A′的橫坐標為1,則A′C的長為_____.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線![]() 交
交![]() 軸
軸![]() 、
、![]() 兩點(
兩點(![]() 在
在![]() 的左側),且
的左側),且![]() ,
,![]() ,與
,與![]() 軸交于
軸交于![]() ,拋物線的頂點坐標為
,拋物線的頂點坐標為![]() .
.
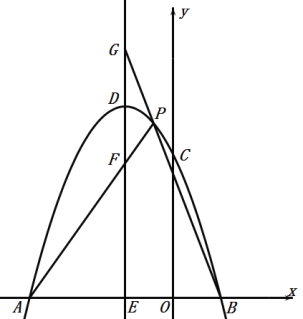
(1)求![]() 、
、![]() 兩點的坐標;
兩點的坐標;
(2)求拋物線的解析式;
(3)過點![]() 作直線
作直線![]() 軸,交
軸,交![]() 軸于點
軸于點![]() ,點
,點![]() 是拋物線上
是拋物線上![]() 、
、![]() 兩點間的一個動點(點
兩點間的一個動點(點![]() 不與
不與![]() 、
、![]() 兩點重合),
兩點重合),![]() 、
、![]() 與直線
與直線![]() 分別交于點
分別交于點![]() 、
、![]() ,當點
,當點![]() 運動時,
運動時,![]() 是否為定值?若是,試求出該定值;若不是,請說明理由.
是否為定值?若是,試求出該定值;若不是,請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】有一個直徑為2m的圓形鐵皮,要從中剪出一個最大的圓心角為90°的扇形ABC.
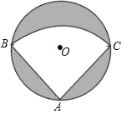
(1)求圖中陰影部分的面積;
(2)若將扇形ABC圍成一個圓錐,則該圓錐的底面半徑最大是多少?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】萬州區(qū)某民營企業(yè)生產的甲、乙兩種產品,已知2件甲商品的出廠總價與3件乙商品的出廠總價相同,3件甲商品的出廠總價比2件乙商品的出廠總價多150元.
(1)求甲、乙商品的出廠單價分別是多少元?
(2)為促進萬州經濟持續(xù)健康發(fā)展,為商家搭建展示平臺,為行業(yè)創(chuàng)造交流機會,2019年萬州區(qū)舉辦了多場商品展銷會.外地一經銷商計劃購進甲商品200件,購進乙商品的數(shù)量是甲的4倍,恰逢展銷會期間該企業(yè)正在對甲商品進行降價促銷活動,甲商品的出廠單價降低了![]() ,該經銷商購進甲的數(shù)量比原計劃增加了
,該經銷商購進甲的數(shù)量比原計劃增加了![]() ,乙的出廠單價沒有改變,該經銷商購進乙的數(shù)量比原計劃減少了
,乙的出廠單價沒有改變,該經銷商購進乙的數(shù)量比原計劃減少了![]() ,結果該經銷商付出的總貨款與原計劃的總貨款恰好相同,求
,結果該經銷商付出的總貨款與原計劃的總貨款恰好相同,求![]() 的值
的值![]() .
.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖1,在等邊三角形ABC中,CD為中線,點Q在線段CD上運動,將線段QA繞點Q順時針旋轉,使得點A的對應點E落在射線BC上,連接BQ,設∠DAQ=α
(0°<α<60°且α≠30°).
(1)當0°<α<30°時,
①在圖1中依題意畫出圖形,并求∠BQE(用含α的式子表示);
②探究線段CE,AC,CQ之間的數(shù)量關系,并加以證明;
(2)當30°<α<60°時,直接寫出線段CE,AC,CQ之間的數(shù)量關系.


![]()
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com